题目内容
【题目】如图,为了测量某电线杆(底部可到达)的高度,准备了如下的测量工具:
①平面镜;②皮尺;③长为2米的标杆;④高为1.5m的测角仪(测量仰角、俯角的仪器),请根据你所设计的测量方案,回答下列问题:

(1)画出你的测量方案示意图,并根据你的测量方案写出你所选用的测量工具;
(2)结合你的示意图,写出求电线杆高度的思路.
【答案】(1)画图见解析;(2)解法见解析.
【解析】
试题分析:(1)根据题意,设计方案如图,选用的测量工具:高为1.5m的测角仪,皮尺;
(2)根据正切函数进行设计测量方法,先测得CA的大小,因为四边形ACDE是矩形;可得DE=AC,AE=CD=1.5;根据相正切函数求得BE,即AB=BE+1.5.
试题解析:(1)测量方案示意图如图;选用的测量工具:高为1.5m的测角仪,皮尺;
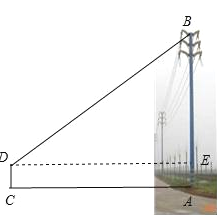
(2)CA(测角仪离电线杆的距离)=a,DC测角仪的高=1.5m,∠BDE(测角仪测的仰角)=α,
根据正切函数;可得:tanα=![]() ;
;
因为DE=CA=a(m),AE=CD=1.5m,
即BE=tanαa(m),
则AB=BE+AE=(tanαa+1.5)m.
故电线杆高度为(tanαa+1.5)米

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目