题目内容
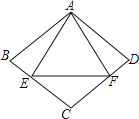
【题目】如图,菱形ABCD与等边△AEF的边长相等,且E、F分别在BC、CD,则∠BAD的度数是( )
A.80° B.90° C.100° D.120°
【答案】C
【解析】
试题分析:根据菱形的性质推出∠B=∠D,AD∥BC,根据平行线的性质得出∠DAB+∠B=180°,根据等边三角形的性质得出∠AEF=∠AFE=60°,AF=AD,根据等边对等角得出∠B=∠AEB,∠D=∠AFD,设∠BAE=∠FAD=x,根据三角形的内角和定理得出方程x+2(180°﹣60°﹣2x)=180°,求出方程的解即可求出答案.
解:∵四边形ABCD是菱形,
∴∠B=∠D,AD∥BC,
∴∠DAB+∠B=180°,
∵△AEF是等边三角形,AE=AB,
∴∠AEF=∠AFE=60°,AF=AD,
∴∠B=∠AEB,∠D=∠AFD,
由三角形的内角和定理得:∠BAE=∠FAD,
设∠BAE=∠FAD=x,
则∠D=∠AFD=180°﹣∠EAF﹣(∠BAE+∠FAD)=180°﹣60°﹣2x,
∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°﹣60°﹣2x)=180°,
解得:x=20°,
∴∠BAD=2×20°+60°=100°,
故选C.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目