题目内容
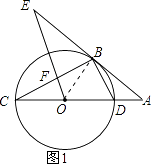
【题目】如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E. 
(1)求证:∠E=∠C;
(2)若⊙O的半径为3,AD=2,试求AE的长;
(3)求△ABC的面积.
【答案】
(1)证明:如图1:连接OB.
∵CD为圆O的直径,
∴∠CBD=∠CBO+∠OBD=90°.
∵AE是圆O的切线,
∴∠ABO=∠ABD+∠OBD=90°.
∴∠ABD=∠CBO.
∵OB=OC,
∴∠C=∠CBO.
∴∠C=∠ABD.
∵OE∥BD,
∴∠E=∠ABD.
∴∠E=∠C
(2)解:∵⊙O的半径为3,AD=2,
∴AO=5,∴AB=4.
∵BD∥OE,
∴BE=OD,
∴BE=3,
∴BE=6,AE=6+4=10
(3)解:∵S△AOE= ![]() AEOB=15,
AEOB=15,
∵∠C=∠E,∠A=∠A,
∴△AOE∽△ABC,
∴ ![]() =(
=( ![]() )2=
)2= ![]() ,
,
∴S△ABC=15× ![]() =
= ![]()
【解析】(1)连接OB.先证明∠ABO、∠CBD均为直角,然后依据同角的余角相等证明∠ABD=∠CBO,接下来,结合等腰三角形的性质和平行线的性质进行证明即可;(2)连接OB,先求得AB的长,然后由平行线分线段成比例定理求得BE的长,最后再△BOE中依据勾股定理可求得OE的长;(3)根据相似三角形的性质即可得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目