题目内容
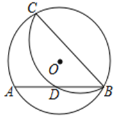
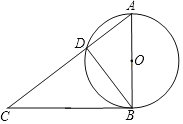
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,连接BD.
(1)求证:∠A=∠CBD.
(2)若AB=10,AD=6,M为线段BC上一点,请写出一个BM的值,使得直线DM与⊙O相切,并说明理由.
【答案】(1)证明见解析;(2)BM=![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用圆周角定理得到∠ADB=90°,然后就利用等角的余角相等得到结论;
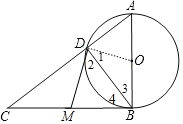
(2)如图,连接OD,DM,先计算出BD=8,OA=5,再证明Rt△CBD∽Rt△BAD,利用相似比得到BC=![]() ,取BC的中点M,连接DM、OD,如图,证明∠2=∠4得到∠ODM=90°,根据切线的判定定理可确定DM为⊙O的切线,然后计算BM的长即可.
,取BC的中点M,连接DM、OD,如图,证明∠2=∠4得到∠ODM=90°,根据切线的判定定理可确定DM为⊙O的切线,然后计算BM的长即可.
(1)∵AB为⊙O直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°.
∵∠ABC=90°,
∴∠CBD+∠ABD=90°,
∴∠A=∠CBD;
(2)BM=![]() .
.
理由如下:
如图,连接OD,DM,
∵∠ADB=90°,AB=10,AD=6,
∴BD=![]() =8,OA=5,
=8,OA=5,
∵∠A=∠CBD,
∵Rt△CBD∽Rt△BAD,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得BC=
,解得BC=![]()
取BC的中点M,连接DM、OD,如图,
∵DM为Rt△BCD斜边BC的中线,
∴DM=BM,
∵∠2=∠4,
∵OB=OD,
∴∠1=∠3,
∴∠1+∠2=∠3+∠4=90°,即∠ODM=90°,
∴OD⊥DM,
∴DM为⊙O的切线,
此时BM=![]() BC=
BC=![]() .
.

练习册系列答案
相关题目