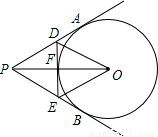
题目内容
如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.求:(1)△PED的周长;(2)∠DOE的度数.
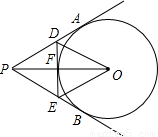
【答案】分析:(1)根据切线长定理,判断出DF=DA,EF=EB,△PED的周长转化为PA+PB,只要求出切线AP的长即可;
(2)根据切线长定理解出∠DOE= ∠AOB,再根据四边形的内角和是360度解答.
∠AOB,再根据四边形的内角和是360度解答.
解答: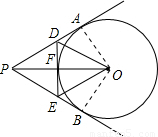 解:如右图所示
解:如右图所示
(1)连接AO,则OA⊥PA,PA=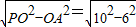 =8,
=8,
∵PA,PB为切线,A,B为切点,EF,EB,DF,DA均与⊙O相切,
∴PA=PB,DA=DF,FE=BE,
∴△PED的周长=PE+EF+FD+PD=PA+PB=2PA=16(cm),
即△PED的周长为16cm;
(2)由切线长性质知:∠AOD=∠DOF,∠EOF=∠EOB,
∴∠DOE= ∠AOB=
∠AOB= (180°-∠APB)=
(180°-∠APB)= (180°-40°)=70°.
(180°-40°)=70°.
点评:此题比较复杂,结合了切线长定理,角平分线的性质,要反复运用切线长定理,将问题转化为勾股定理和角平分线的性质解答.
(2)根据切线长定理解出∠DOE=
 ∠AOB,再根据四边形的内角和是360度解答.
∠AOB,再根据四边形的内角和是360度解答.解答:
 解:如右图所示
解:如右图所示(1)连接AO,则OA⊥PA,PA=
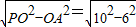 =8,
=8,∵PA,PB为切线,A,B为切点,EF,EB,DF,DA均与⊙O相切,
∴PA=PB,DA=DF,FE=BE,
∴△PED的周长=PE+EF+FD+PD=PA+PB=2PA=16(cm),
即△PED的周长为16cm;
(2)由切线长性质知:∠AOD=∠DOF,∠EOF=∠EOB,
∴∠DOE=
 ∠AOB=
∠AOB= (180°-∠APB)=
(180°-∠APB)= (180°-40°)=70°.
(180°-40°)=70°.点评:此题比较复杂,结合了切线长定理,角平分线的性质,要反复运用切线长定理,将问题转化为勾股定理和角平分线的性质解答.

练习册系列答案
相关题目
 如图所示,一个半径为
如图所示,一个半径为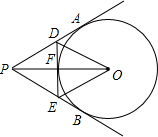 如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.
如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.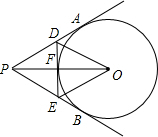 如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.
如图所示,过半径为6cm的⊙O外一点P引圆的切线PA,PB,连接PO交⊙O于F,过F作⊙O的切线,交PA,PB分别于D,E,如果PO=10cm,∠APB=40°.