题目内容
如图，在边长为1的正方形ABCD中，P是射线BC上的一个动点，过P作DP的垂线交射线AB于点E．设BP=x，AE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）分析：根据已知条件得到函数的解析式，然后根据函数解析式求函数图象．
解答：解：∵∠EPB+∠DPC=90°，
∴∠EPB=∠PDC
∴△EBP∽△PCD，
∴
=
即：
=
∴EB=x-x2
∴AE=1-BE=1-x+x2，
故选A．
∴∠EPB=∠PDC
∴△EBP∽△PCD，
∴
| EB |
| BP |
| PC |
| CD |
即：
| EB |
| x |
| 1-x |
| 1 |
∴EB=x-x2
∴AE=1-BE=1-x+x2，
故选A．
点评：本题考查了动点问题，能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
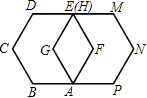如图，如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合，那么点B的对应点是点
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
如图，将边长为3的正六边形A1A2A3A4A5A6，在直线l上由图1的位置按顺时针方向向右作无滑动滚动，当A1第一次滚动到图2位置时，顶点A1所经过的路径的长为（ ）
已知：如图，在边长为a的正△ABC中，分别以A，B，C点为圆心，
长为半径作
，
，
，求阴影部分的面积．
长为半径作
，
，
，求阴影部分的面积．