��Ŀ����
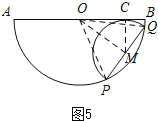
����Ŀ����ͼ����ԲO��ֱ��AB��4���Գ�Ϊ2����PQΪֱ�������O��������ԲM������P���ڻ�AQ��������A���غϣ���Q�����B���غϣ�
��1����AP�ij��뻡QB�ij�֮��Ϊ��ֵl����ֱ��д��l��ֵ��
��2����ֱ��д����M��AB�������룬��ʱ��P��A��ľ��룻��M��AB����С���룬��ʱ��ԲM�Ļ���AB��Χ�ɵķ��ͼ�������
��3������ԲM��AB����ʱ����AP�ij���
��ע����������У�cos 35�㣽![]() ��cos 55�㣽
��cos 55�㣽![]() ��
��

���𰸡���1��![]() ����2��
����2��![]() ��2��
��2�� ![]() ��
�� ![]() ����3����AP�ij�Ϊ
����3����AP�ij�Ϊ![]() ��
��![]() ��
��
�������������������1����ԲO�ij����ǹ̶�����ģ�����PQҲ�Ƕ�ֵ������![]() �ij���Ҳ�ǹ̶�ֵ������
�ij���Ҳ�ǹ̶�ֵ������![]() ��
��![]() �ij�֮��Ϊ��ֵ��
�ij�֮��Ϊ��ֵ��
��2������M��MC��AB�ڵ�C����C��O�غ�ʱ��M��AB�ľ������ʱ����AOP=60����AP=2����Q��B�غ�ʱ��M��AB�ľ�����С����ʱΧ�ɵķ��ͼ���������������DMB�������ȥ��DMB��������ɣ�
��3������ԲM��AB����ʱ����ʱMC=1���ҷ���������������ۣ���C���߶�OA�ϣ���C���߶�OB�ϣ�Ȼ��ֱ�Ƴ�![]() �ij���
�ij���
���������
(1)��ͼ1,����OP��OQ,

��AB=4��
��OP=OQ=2��
��PQ=2��
���OPQ�ǵȱ������Σ�
���POQ=60����
��![]() ��
��
�֡߰�ԲO�ij�Ϊ�� ![]() �С�4=2����
��4=2����
��![]() =2��
=2�� ![]() ��
��
��![]() ��
��
��2����ͼ2������M��MC��AB�ڵ�C������OM��
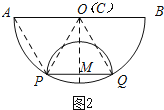
��OP=2,PM=1,
���ɹ��ɶ�����֪��OM=![]() ��
��
��C��O�غ�ʱ��
M��AB�ľ������,���ֵΪ![]() ��
��
����AP��
��ʱ��OM��AB��
���AOP=60��
��OA=OP��
���AOP�ǵȱ������Σ�
��
��ͼ3,��Q��B�غ�ʱ,����DM��
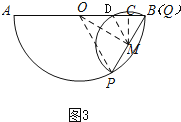
�ߡ�MOQ=30����
��MC=![]() OM=
OM=![]() ��
��
��ʱ,M��AB�ľ�����С,��СֵΪ![]() ��
��
���ʱ��ԲM��AB���ڵ�D��
DM=MB=1��
�ߡ�ABP=60����
���DMB�ǵȱ������Σ�
���DMB=60����
������DMB������� ![]() ��
��
��DMB������� ![]() MCDB=
MCDB=![]() ��
��
���ԲM�Ļ���AB��Χ�ɵķ��ͼ�����Ϊ�� ![]() ��
��
��3������ԲM��AB����ʱ,
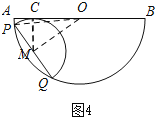
��ʱ��MC=1��
��ͼ4������C���߶�OA��ʱ��
��Rt��OCM��
�ɹ��ɶ�������ã�OC=![]() ��
��
��cos��AOM=![]() ��
��
���AOM=35����
�ߡ�POM=30����
���AOP=��AOM��POM=5����
��![]() ��
��
����C���߶�OB��ʱ��
��ʱ,��BOM=35��,
�ߡ�POM=30����
���AOP=180��POM��BOM=115��
��![]() ��
��
���ϣ���AP�ij�Ϊ![]() ��
��![]() ��
��

 ��ѧ��������������Ͼ���ѧ������ϵ�д�
��ѧ��������������Ͼ���ѧ������ϵ�д�����Ŀ����һ���������У�С���ռ���ij���������˶����Ŷ���20����Աһ�����ߵIJ�������¼���£�
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850

����20�����ݰ����1000���з��飬��ͳ�������������������в�������ͳ��ͼ����
��������ͳ�Ʊ�
��� | �������� | Ƶ�� |
A | 5500��x��6500 | 2 |
B | 6500��x��7500 | 10 |
C | 7500��x��8500 | m |
D | 8500��x��9500 | 3 |
E | 9500��x��10500 | n |
�����������Ϣ����������⣺
��1����m��n��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����20�����������˶����Ŷӳ�Աһ�����߲�������λ��������һ�飿
��4�������Ŷӹ���120�ˣ����������һ�����߲���������7500����������