题目内容
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD交OD的延长线于点A,连接BC,∠B=∠A=30°,BD=4 ![]() .
.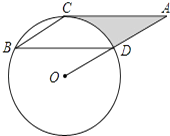
(1)求证:AC是⊙O的切线;
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积.(结果保留π)
【答案】
(1)证明:连接OC交BD于点E,
∵∠B=30°,
∴∠COD=2∠B=60°,
又∵∠A=30°,
∴∠ACO=90°,
即OC⊥AC,
∴AC是⊙O的切线.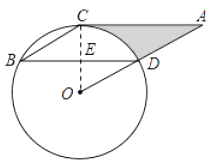
(2)解:∵AC∥BD,∠ACO=90°,
∴∠OED=∠ACO,
即OC⊥BD,
又∵BD=4![]() ,
,
∴DE=![]() BD=2
BD=2![]() ,
,
又∵sin∠OCD=sin60°=![]() ,
,
∴![]() ,
,
∴OD=4,
又∵tan∠OCD=tan60°=![]() ,
,
∴![]() ,
,
∴AC=4![]() ,
,
∴S阴=S△OAC-S扇形OCD
∴S阴=![]() ×AC×OC-
×AC×OC-![]() ,
,
∴S阴=![]() ×4
×4![]() ×4-
×4-![]() ,
,![]() ∴S阴=8
∴S阴=8![]() -
-![]() .
.
【解析】(1)连接OC交BD于点E,由同弧所对的圆心角等于圆周角的两倍得出∠COD=2∠B=60°,从而得出∠ACO=90°,即AC是⊙O的切线.
(2)由两直线平行,同位角相等得出∠OED=∠ACO=90°,再根据垂径定理得出DE=![]() BD=2
BD=2![]() ,在Rt△ODE和Rt△OAC中,由锐角三角函数得出
,在Rt△ODE和Rt△OAC中,由锐角三角函数得出
OD=4,AC=4![]() ,再由S阴=S△OAC-S扇形OCD计算即可.
,再由S阴=S△OAC-S扇形OCD计算即可.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目