题目内容
已知a、b满足a3-3a2+5a=1,b3-3b2+5b=5,试求a+b的值.
解:∵a3-3a2+5a=1
∴(a-1)3+2(a-1)+2=0
∵b3-3b2+5b=5
∴(b-1)3+2(b-1)-2=0
设a-1=x,b-1=y
则x3+2x+2=0,y3+2y-2=0
两式相加可得x3+y3+2(x+y)=0
化简整理得(x+y)(
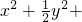
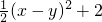 )=0
)=0
∴x+y=0
即a-1+b-1=0
∴a+b=2.
分析:对a3-3a2+5a=1,b3-3b2+5b=5分别进行整理后,将(a-1)与(b-1)看成整体,再化简求出(a-1)与(b-1)之间关系,即可求出a+b的值.
点评:本题考查因式分解的运用,有公因式时,要先考虑提取公因式;注意运用整体代入法求解.
∴(a-1)3+2(a-1)+2=0
∵b3-3b2+5b=5
∴(b-1)3+2(b-1)-2=0
设a-1=x,b-1=y
则x3+2x+2=0,y3+2y-2=0
两式相加可得x3+y3+2(x+y)=0
化简整理得(x+y)(

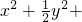
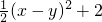 )=0
)=0∴x+y=0
即a-1+b-1=0
∴a+b=2.
分析:对a3-3a2+5a=1,b3-3b2+5b=5分别进行整理后,将(a-1)与(b-1)看成整体,再化简求出(a-1)与(b-1)之间关系,即可求出a+b的值.
点评:本题考查因式分解的运用,有公因式时,要先考虑提取公因式;注意运用整体代入法求解.

练习册系列答案
相关题目