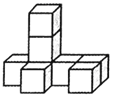
题目内容
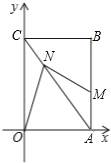
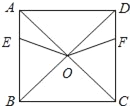
【题目】已知正方形ABCD,AB=8,点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t.
(1)求证:OE=OF.
(2)在点E、F的运动过程中,连结AF.设线段AE、OE、OF、AF所形成的图形面积为S.
探究:①S的大小是否会随着运动时间为t的变化而变化?若会变化,试求出S与t的函数关系式;若不会变化,请说明理由.
②连结EF,当运动时间为t为何值时,△OEF的面积恰好等于的![]() S.
S.
【答案】(1)见解析(2)①见解析②t为时
【解析】试题分析:(1)根据正方形的性质得出OA=OD,∠EAO=∠FDO=45°,求出AE=DF=t,根据SAS推出△EAO≌△FDO即可;
(2)①延长EO交DC于M,求出△AOE≌△COM,根据全等三角形的性质得出AE=CM=t,根据S=S四边形AEMF﹣S△FOM求出即可;
②根据全等得出OE=OM,求出S△EOF=S△EFM=16﹣4t,即可得出方程16﹣4t=×16,求出即可.
(1)证明:∵四边形ABCD是正方形,
∴OA=OD,∠EAO=∠FDO=45°,
∵点E、F分别从点A、D同时出发,以每秒1m的速度分别沿着线段AB、DC向点B、C方向的运动,设运动时间为t,
∴AE=DF=t,
在△EAO和△FDO中
![]()
∴△EAO≌△FDO(SAS),
∴OE=OF;
(2)解:①S的大小不会随着运动时间为t的变化而变化,

理由是:延长EO交DC于M,
∵四边形ABCD是正方形,
∴∠OAE=∠MCO=45°,OA=OC,
在△AOE和△COM中
![]()
∴△AOE≌△COM(ASA),
∴AE=CM=t,
∴S=S四边形AEMF﹣S△FOM
=(t+8﹣t﹣t)8﹣×(8﹣t﹣t)4
=16,
所以S的大小不会随着运动时间为t的变化而变化;
②∵△AOE≌△COM,
∴OE=OM,
∴S△EOF=S△FOM=S△EFM=×(8﹣t﹣t)8=16﹣4t,
∵△OEF的面积恰好等于的S,
∴16﹣4t=×16,
解得:t=,
即当运动时间为t为时,△OEF的面积恰好等于的S.