题目内容
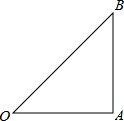
如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
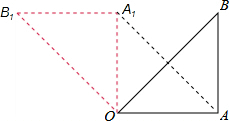
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.
(1)请你画出将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1;
(2)线段OA1的长度是______,∠AOB1的度数是______;
(3)连接AA1,求证:四边形OAA1B1是平行四边形.

(1)△OA1B1如图所示.
(2)根据旋转的性质知,OA1=OA=6.
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠BOB1=90°.
∵在Rt△OAB中,∠OAB=90°,OA=AB=6,
∴∠BOA=∠OBA=45°,
∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°.
故答案是:6,135°;
(3)证明:根据旋转的性质知,△OA1B1≌△OAB,
则∠OA1B1=∠OAB=90°,A1B1=AB,
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠A1OA=90°,
∴∠OA1B1=∠A1OA,
∴A1B1∥OA.
又∵OA=AB,
∴A1B1=OA,
∴四边形OAA1B1是平行四边形.
(2)根据旋转的性质知,OA1=OA=6.
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠BOB1=90°.
∵在Rt△OAB中,∠OAB=90°,OA=AB=6,
∴∠BOA=∠OBA=45°,
∴∠AOB1=∠BOB1+∠BOA=90°+45°=135°,即∠AOB1的度数是135°.
故答案是:6,135°;
(3)证明:根据旋转的性质知,△OA1B1≌△OAB,
则∠OA1B1=∠OAB=90°,A1B1=AB,
∵将△OAB绕点O沿逆时针方向旋转90°,得到的△OA1B1,
∴∠A1OA=90°,
∴∠OA1B1=∠A1OA,
∴A1B1∥OA.
又∵OA=AB,
∴A1B1=OA,
∴四边形OAA1B1是平行四边形.


练习册系列答案
相关题目





 点上,在方格纸中建立平面直角坐标系如图所示.
点上,在方格纸中建立平面直角坐标系如图所示.

