题目内容
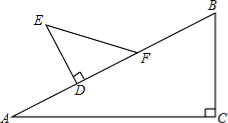
【题目】如图,在△ABC中,∠B=70°,∠BAC=30°,将△ABC绕点C顺时针旋转得到△EDC,当点B的对应点D恰好落在AC边上时,∠CAE的度数为___________.

【答案】50°
【解析】
由旋转可得∠CDE=∠B=70°,∠CED=∠BAC=30°,CA=CE,则∠CAE=∠CEA,再由三角形的外角性质可得∠CDE=∠CAE+∠AED可求出∠CAE的度数.
∵△ABC绕点C顺时针旋转得到△EDC
∴∠CDE=∠B=70°,∠CED=∠BAC=30°,CA=CE,
∴∠CAE=∠CEA,
则∠AED=∠CEA-30°
又∵∠CDE=∠CAE+∠AED
即∠CAE+∠CAE-30°=70°
解得∠CAE=50°
故答案为:50°.

练习册系列答案
相关题目