题目内容
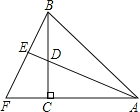
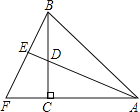
【题目】如图,AC=BC,∠ACB=90°,AE平分∠BAC交BC于点D,BF⊥AE,交AC的延长线于点F,且垂足为E,则下列结论①AD=BF;②BF=AF;③AC+CD=AB;④AB=BF:⑤AD=2BE.其中正确的结论有( )个
A. 5B. 4C. 3D. 2
【答案】C
【解析】
根据∠ACB=90°,BF⊥AE,得出∠ACB=∠BED=∠BCF=90°,推出∠F=∠ADC,证△BCF≌△ACD,根据全等三角形的性质即可判断①②;假如AC+CD=AB,求出∠F+∠FBC=90°,即可判断③④,证根据全等三角形的判定ASA得出△BEA≌△FEA,推出BE=EF,即可判断⑤.
解:∵∠ACB=90°,BF⊥AE,
∴∠ACB=∠BED=∠BCF=90°,
∴∠F+∠FBC=90°,∠BDE+∠FBC=90°,
∴∠F=∠BDE,
∵∠BDE=∠ADC,
∴∠F=∠ADC,
∵AC=BC,
∴△BCF≌△ACD,
∴AD=BF,∴①正确;
∵AF>AD,
∴BF≠AF②错误;
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
∵△BCF≌△ACD,
∴CD=CF,
∴AC+CD=AF,
又∵AB=AF,
∴AC+CD=AB.
∴③正确;
∵BF=AC,AC<AF=AB,
∴AB>BF,
∴④错误;
由△BCF≌△ACD,
∴AD=BF,
∵AE平分∠BAF,AE⊥BF,
∴∠BEA=∠FEA=90°,∠BAE=∠FAE,
∵AE=AE,∴△BEA≌△FEA,
∴BE=EF,
∴⑤正确;
综上所述,正确的结论是:①③⑤,共有3个.
故选:C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目