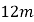Question

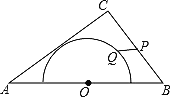
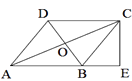
【题目】如图，在四边形ABCD中，AB∥DC，AB=AD，对角线AC、BD相交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，若AB=，BD=2，则OE的长等于________．

Answer 1

【答案】

【解析】

先判断出∠OAB=∠DCA，进而判断出∠DAC=∠DAC，得出CD=AD=AB，即可得出四边形ABCD是菱形；再判断出OE=OA=OC，再求出OB=1，利用勾股定理求出OA，即可得出结论．

（1）∵AB∥CD，

∴∠OAB=∠DCA，

∵AC为∠DAB的平分线，

∴∠OAB=∠DAC，

∴∠DCA=∠DAC，

∴CD=AD=AB，

∵AB∥CD，

∴四边形ABCD是平行四边形，

∵AD=AB，

∴ABCD是菱形；

∴OA=OC，BD⊥AC，∵CE⊥AB，

∴OE=OA=OC，

∵BD=2，

∴OB=BD=1，

在Rt△AOB中，AB=，OB=1，

∴OA==2，

∴OE=OA=2．