题目内容
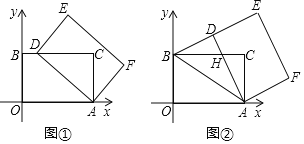
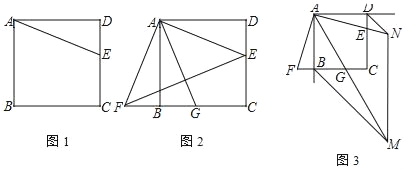
【题目】如图,点E是正方形ABCD中CD边上任意一点,AB=4,以点A为中心,把△ADE顺时针旋转90°得到△AD′F
(1)画出旋转后的图形,求证:点C、B、F三点共线;
(2)AG平分∠EAF交BC于点G.
①如图2,连接EF.若BG:CE=5:6,求△AEF的面积;
②如图3,若BM、DN分别为正方形的两个外角角平分线,交AG、AE的延长线于点M、N.当MM∥DC时,直接写出DN的长.
【答案】(1)详见解析;(2)①![]() ②
②![]() .
.
【解析】
(1)旋转后的图形如图1中所示,利用旋转不变性即可解决问题;
(2)①如图2中,连接EG.首先证明EG=BG+DE,设BG=5k,CE=6k,则DE=4-6k,CG=4-5k,EG=4-k,在Rt△EGC中,根据EG2=EC2+CG2即可解决问题;
②如图3中,连接EG,延长MN交AD的延长线于点P,作MQ⊥AB交AB的延长线于点Q.由题意可知:△PDN,△BMQ都是等腰直角三角形,设DP=PN=x,BG=a,DE=b.想办法构建方程组即可解决问题.
(1)证明:旋转后的图形如图1中所示,

∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°,
∵∴点D′与点B重合,
∵∠AD′F=90°,
∴∠AD′F+′AD′C=180°,
∴C,B,F共线.
(2)①解:如图2中,连接EG.
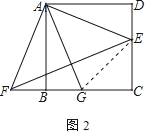
∵∠BAF=∠DAE,
∴∠EAF=∠DAB=90°,
∵AG平分∠EAF,
∴∠EAG=![]() ×90°=45°,
×90°=45°,
∴∠FAG=∠FAB+∠BAG=∠BAG+∠DAE=45°,
∴∠FAG=∠EAG,
∵AG=AG,AF=AE,
∴△GAE≌△GAF(SAS),
∴FG=EG,
∴EG=BF+BG=DE+BG,
∵BG:CE=5:6,
∴可以假设BG=5k,CE=6k,则DE=4﹣6k,CG=4﹣5k,EG=4﹣k,
在Rt△EGC中,∵EG2=EC2+CG2,
∴(4﹣k)2=(6k)2+(4﹣5k)2,
∴k=![]() ,
,
∴DE=![]() ,
,
∴AE=AF=![]() ,
,
∴S△AEF=![]() AEAF=
AEAF=![]() .
.
②解:如图3中,连接EG,延长MN交AD的延长线于点P,作MQ⊥AB交AB的延长线于点Q.

由题意可知:△PDN,△BMQ都是等腰直角三角形,设DP=PN=x,BG=a,DE=b.
∵四边形AQMP是矩形,
∴MQ=BQ=AP=4+x,
∵DE∥PN,
∴![]() ,即
,即![]() ①,
①,
∵BG∥MQ,
∴![]() ,即
,即![]() ②
②
在Rt△BCG中,∵EG2=EC2+CG2,
∴(a+b)2=(4-a)2+(4-b)2 ③,
由①②③可得x=2或-2(舍弃)
∴DN=![]() x=2
x=2![]() .
.