题目内容
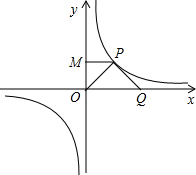 如图,p是双曲线上一点,直线PQ交x轴于Q点,PM∥x轴交y轴于M,△OPM的面积为1.
如图,p是双曲线上一点,直线PQ交x轴于Q点,PM∥x轴交y轴于M,△OPM的面积为1.(1)求双曲线的解析式;
(2)若△OPQ是等腰直角三角形,求Q点的坐标.
分析:(1)此题只需根据反比例函数系数k的几何意义,由△OPM的面积确定出比例系数k的值即可;
(2)此题只需根据△OPQ是等腰直角三角形,先确定出OP的长,再得出OQ的长,即可得出Q点的坐标.
(2)此题只需根据△OPQ是等腰直角三角形,先确定出OP的长,再得出OQ的长,即可得出Q点的坐标.
解答:解:(1)设p(m,n),双曲线的解析式为y=
(k>0);
则
mn=1,即mn=2;
又∵n=
,即k=mn=2,∴y=
;
(2)由△OPQ是等腰直角三角形,则OP是∠xoy的平分线,
∴m=n;
又mn=2,则m=n=
.
∴OP=2,则OQ=2
;
即Q(2
,0).
| k |
| x |
则
| 1 |
| 2 |
又∵n=
| k |
| m |
| 2 |
| x |
(2)由△OPQ是等腰直角三角形,则OP是∠xoy的平分线,
∴m=n;
又mn=2,则m=n=
| 2 |
∴OP=2,则OQ=2
| 2 |
即Q(2
| 2 |
点评:本题考查了反比例函数的综合应用,要注意数形结合思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
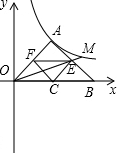
 (2013•海沧区一模)如图,已知双曲线
(2013•海沧区一模)如图,已知双曲线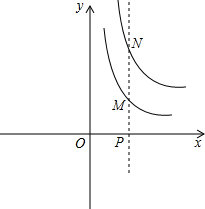 【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段)
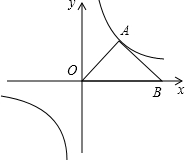
【倾听理解】(这是一次数学活动课上,师生利用“几何画板”软件探究函数性质的活动片段) 如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=
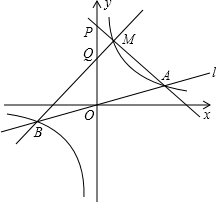
如图,在平面直角坐标系中,直线y=-2x+2与x轴、y轴分别相交于点A,B,四边形ABCD是正方形,反比例函数y=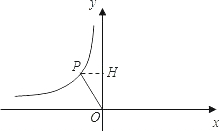 如图是反比例函数
如图是反比例函数