题目内容
已知b-a＞0，且a≥0，那么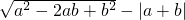
- A.化简为0
- B.化简为-2b
- C.化简为-2a
- D.不能再化简
C
分析：利用已知条件b-a＞0，且a≥0，对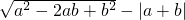开根号求解．
解答：由b-a＞0．且a≥0．则b＞a≥0，得a+b＞0，又∵b-a＞0，
∴a-b＜0
∴原式=|a-b|-|a+b|=-（a-b）-（a+b）=-2a．
∴故选C．
点评：此题主要考查二次根式的性质和化简，计算时要仔细，是一道基础题．
分析：利用已知条件b-a＞0，且a≥0，对
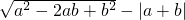开根号求解．解答：由b-a＞0．且a≥0．则b＞a≥0，得a+b＞0，又∵b-a＞0，
∴a-b＜0
∴原式=|a-b|-|a+b|=-（a-b）-（a+b）=-2a．
∴故选C．
点评：此题主要考查二次根式的性质和化简，计算时要仔细，是一道基础题．
练习册系列答案
相关题目
如图，已知∠1，∠2互为补角，且∠3=∠B，