题目内容
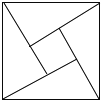
【题目】“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若(a＋b)2＝21，大正方形的面积为13，则小正方形的面积为
A. 3B. 4C. 5D. 8
【答案】C
【解析】
观察图形可知，大正方形的面积=4个直角三角形的面积+小正方形的面积，利用已知（a+b）2=21，大正方形的面积为13，可以得出直角三角形的面积，进而求出答案．
解：由题意可知：中间小正方形的边长为：a-b
∴每一个直角三角形的面积为：
ab
∴4×ab+（a-b）2=13
∴2ab+a2-2ab+b2=13
∴a2+b2=13，
∵(a＋b)2＝a2+2ab+b2=21，
∴ab=4
∴（a-b）2=a2-2ab+b2=13-8=5 .
故选：C.
练习册系列答案
阅读快车系列答案
相关题目
