题目内容
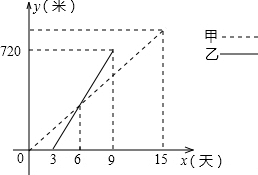
(1)A、B两村之间的公路进行对接修筑,甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.如图1甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:
①乙工程队每天修公路多少米?
②分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式;
③若乙工程队后来进入施工后,不提前离开,直到公路对接完工,那么施工过程共需几天?
(2)如图2直线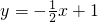 分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a,
分别与x轴、y轴交于点A、B,在第一象限取点C,使△ABC成为等腰直角三角形;如果在第二象限内有一点P(a, ),使△ABP的面积与Rt△ABC的面积相等,求a的值.
),使△ABP的面积与Rt△ABC的面积相等,求a的值.
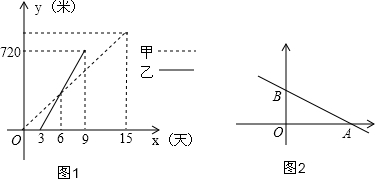
解:(1)①∵乙工程队修了720米,用时9-3=6天,
∴乙工程队每天修公路120米.
②设乙工程队y与x之间的函数关系式为y=kx+b,直线过点(3,0)、(9,720)
代入得y乙=120x-360(3≤x≤9)
设甲工程队y与x之间的函数关系式为y=kx,由y乙 求得过点(6,360)
代入得y甲=60x(0≤x≤15)
③∵乙工程队修了720米,甲工程队修了15×60=900米,
∴公路总长1620米,
前3天甲单独修了180米,
∴甲乙合作修了1440米,
∴(120+60)x=1440,
x=8,
∴这个施工过程共需3+8=11(天)
(2)①由题意得A(2,0)、B(0,1),
∴OA=2,OB=1,
在Rt△AOB中,由勾股定理,得
AB= .
.
以A或B为三角形的直角顶点时,
S△ABC= ,
,
连接PA、PB、PO,
则S△PBA=S△PBO+S△ABO-S△POA
=- +1-
+1- =-
=- +
+ ,
,
当- +
+ =
= ,
,
解得a=-4
②以C为直角顶点时,S△ABC=
当- +
+ =
= ,
,
解得:a=- .
.
分析:(1)①运用乙工程队6天修的长度除以时间就可以求出乙工程队每天修的米数;
②由(1)就可以求出乙工程队3天修的米数,根据待定系数法就可以直接求出甲、乙的解析式;
③运用甲乙合修的时间加上甲先修的时间就可以求出共需的时间;
(2)先运用勾股定理求出AB的长,根据等腰直角三角形的性质分类讨论就可以求出结论.
点评:本题考查了工程问题的数量关系,工作总量=工作效率×工作时间的运用,待定系数法求一次函数的解析式的运用,三角形的面积公式的运用及等腰直角三角形的性质的运用,解答时理解函数图象的意义和抓住工程问题的基本数量关系是关键.

∴乙工程队每天修公路120米.
②设乙工程队y与x之间的函数关系式为y=kx+b,直线过点(3,0)、(9,720)
代入得y乙=120x-360(3≤x≤9)
设甲工程队y与x之间的函数关系式为y=kx,由y乙 求得过点(6,360)
代入得y甲=60x(0≤x≤15)
③∵乙工程队修了720米,甲工程队修了15×60=900米,
∴公路总长1620米,
前3天甲单独修了180米,
∴甲乙合作修了1440米,
∴(120+60)x=1440,
x=8,
∴这个施工过程共需3+8=11(天)
(2)①由题意得A(2,0)、B(0,1),
∴OA=2,OB=1,
在Rt△AOB中,由勾股定理,得
AB=
 .
.以A或B为三角形的直角顶点时,
S△ABC=
 ,
,连接PA、PB、PO,
则S△PBA=S△PBO+S△ABO-S△POA
=-
 +1-
+1- =-
=- +
+ ,
,当-
 +
+ =
= ,
,解得a=-4
②以C为直角顶点时,S△ABC=

当-
 +
+ =
= ,
,解得:a=-
 .
.分析:(1)①运用乙工程队6天修的长度除以时间就可以求出乙工程队每天修的米数;
②由(1)就可以求出乙工程队3天修的米数,根据待定系数法就可以直接求出甲、乙的解析式;
③运用甲乙合修的时间加上甲先修的时间就可以求出共需的时间;
(2)先运用勾股定理求出AB的长,根据等腰直角三角形的性质分类讨论就可以求出结论.
点评:本题考查了工程问题的数量关系,工作总量=工作效率×工作时间的运用,待定系数法求一次函数的解析式的运用,三角形的面积公式的运用及等腰直角三角形的性质的运用,解答时理解函数图象的意义和抓住工程问题的基本数量关系是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
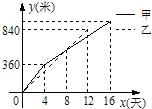 某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.
某县在实施“村村通”工程中,决定在A、B两村之间修筑一条公路,甲、乙两个工程队分别从A、B两村同时相向开始修筑.施工期间,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到道路修通.下图是甲、乙两个工程队所修道路的长度y(米)与修筑时间x(天)之间的函数图象,请根据图象所提供的信息,求该公路的总长度.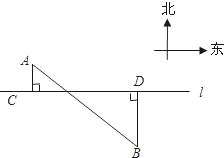 的距离相等,请用尺规在图中作出点P的位置(保留清晰的作图痕迹,并简要写明作法).
的距离相等,请用尺规在图中作出点P的位置(保留清晰的作图痕迹,并简要写明作法).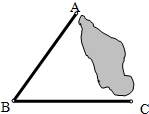 16、如图,A.B.C为三个村庄,A.B两村及B.C两村之间通有公路,A.C两村被一个湖隔开.现欲建一个中转站P,使得P到B.C两村的距离相等,且到两条公路的距离也相等.(不用写作法,保留作图痕迹.)
16、如图,A.B.C为三个村庄,A.B两村及B.C两村之间通有公路,A.C两村被一个湖隔开.现欲建一个中转站P,使得P到B.C两村的距离相等,且到两条公路的距离也相等.(不用写作法,保留作图痕迹.)