题目内容
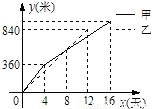
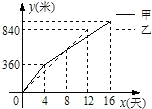某县在实施“村村通”工程中，决定在A、B两村之间修筑一条公路，甲、乙两个工程队分别从A、B两村同时相向开始修筑．施工期间，乙队因另有任务提前离开，余下的任务由甲队单独完成，直到道路修通．下图是甲、乙两个工程队所修道路的长度y（米）与修筑时间x（天）之间的函数图象，请根据图象所提供的信息，求该公路的总长度．
分析：由图象可知，乙铺了12天，共840米，甲铺路16天，要求甲铺路多少，需求出他的第二部分的解析式，因此需求出乙过点（12，840）的解析式，然后求出两直线的交点（8，560），再利用点（4，360），求出甲的解析式，令其中x=16，即可求出甲铺路多少，然后就可求出答案．
解答：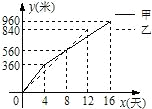
解：设y乙=kx（0≤x≤12），
∵840=12k，
∴k=70．
∴y乙=70x．（2分）
当x=8时，y乙=560．（3分）
设y甲=mx+n（4≤x≤16），
∴
，
解得
，
∴y甲=50x+160（4≤x≤16）．（5分）
当x=16时，y甲=50×16+160=960．（6分）
∴840+960=1800米．
故该公路全长为1800米．（8分）
解：设y乙=kx（0≤x≤12），∵840=12k，
∴k=70．
∴y乙=70x．（2分）
当x=8时，y乙=560．（3分）
设y甲=mx+n（4≤x≤16），
∴
|
解得
|
∴y甲=50x+160（4≤x≤16）．（5分）
当x=16时，y甲=50×16+160=960．（6分）
∴840+960=1800米．
故该公路全长为1800米．（8分）
点评：本题需利用待定系数法求出函数的解析式，然后求出特殊点的坐标，即可解决问题．
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
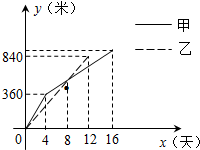）与修筑时间x（天）之间的函数图象，请根据图象所提供的信息，解答下列问题：
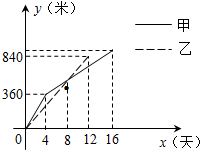）与修筑时间x（天）之间的函数图象，请根据图象所提供的信息，解答下列问题：