题目内容
【题目】如图,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
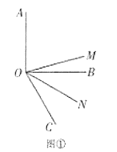
(1)如图①,当![]() 是直角,
是直角,![]() 时,
时,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
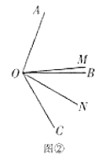
(2)如图②,当![]() ,
,![]() 时,猜想:
时,猜想:![]() 的度数与
的度数与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
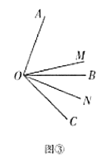
(3)如图③,当![]() ,
,![]() (
(![]() 为锐角)时,猜想:
为锐角)时,猜想:![]() 的度数与
的度数与![]() ,
,![]() 有怎样的数量关系?请写出结论,并说明理由.
有怎样的数量关系?请写出结论,并说明理由.
【答案】(1) 30°,75°,45°;(2) ∠MON=![]()
![]() ,理由见解析;(3) ∠MON=
,理由见解析;(3) ∠MON=![]()
![]() ,与
,与![]() 无关,理由见解析
无关,理由见解析
【解析】
(1)因为ON平分∠BOC,OM是∠AOC的平分线,根据角平分线的性质即可得出∠NOC=![]() ∠BOC,∠AOM=∠MOC=
∠BOC,∠AOM=∠MOC=![]() ∠AOC,再结合已知条件即可求解;
∠AOC,再结合已知条件即可求解;
(2) ∠MON=![]()
![]() ,根据题目已知条件可以得到∠MOC=
,根据题目已知条件可以得到∠MOC=![]() ∠AOC,∠NOC=
∠AOC,∠NOC=![]() ∠BOC,代入题目条件即可得出结果;
∠BOC,代入题目条件即可得出结果;
(3) ∠MON=![]()
![]() ,与
,与![]() 无关,根据题目已知条件表示出∠AOC,再利用角平分线的性质即可得出结果.
无关,根据题目已知条件表示出∠AOC,再利用角平分线的性质即可得出结果.
解:(1)∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ×60°=30°,
×60°=30°,
∵OM是∠AOC的平分线,
∴∠AOM=∠MOC=![]() ∠AOC,
∠AOC,
∵∠AOC=∠AOB+∠BOC=90°+60°=150°,
∴∠MOC=75°,
∴∠MON=∠MOC-∠NOC=75°-30°=45°,
故答案为:30°,75°,45°
(2)∠MON=![]()
![]() .
.
∵∠AOC=∠AOB+∠BOC=![]() +60°,OM是∠AOC的平分线,
+60°,OM是∠AOC的平分线,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (
(![]() +60°)=
+60°)=![]()
![]() +30°,
+30°,
∵ON平分∠BOC,
∴∠NOC=![]() ∠BOC=
∠BOC=![]() ×60°=30°,
×60°=30°,
∴∠MON=∠MOC-∠NOC=![]()
![]() +30°-30°=
+30°-30°=![]()
![]() ;
;
(3)∠MON=![]()
![]() ,与
,与![]() 无关.
无关.
∵∠AOB=![]() ,∠BOC=
,∠BOC=![]() ,
,
∴∠AOC=![]() +
+![]() ,
,
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC=![]() ∠AOC=
∠AOC=![]() (
(![]() +
+![]() ),∠NOC=
),∠NOC=![]() ∠BOC=
∠BOC=![]()
![]() ,
,
∴∠MON=∠MOC-∠NOC=![]() (
(![]() +
+![]() )-
)-![]()
![]() =
=![]()
![]() .
.