题目内容
如图，过△ABC内一点M做各边的平行线与各边分别交于D，E，F，G，L，N各点．求证：
+
+
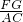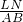=2．
证明：根据题意，DE∥BC，
∴△ADE∽△ABC
∴=
；
∵△BFG∽△BAC
∴=
；
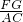∵AFML是平行四边形，
∴LM=AF；同理，MN=BD；
则=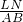
，∴++=
=
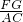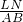=2．
分析：若将所求的等式左边进行通分，解起来会非常麻烦，所以要通过相似三角形得出的对应成比例相等来求证；根据△ADE∽△ABC、△BFG∽△BAC得出的对应成比例线段，用分母为AB的式子替换掉、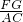，然后再通过这些线段和AB的关系来证明所求的结论．
点评：此题主要考查了平行四边形的性质以及相似三角形的判定和性质．
∴△ADE∽△ABC
∴
=；∵△BFG∽△BAC
∴
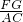=；∵AFML是平行四边形，
∴LM=AF；同理，MN=BD；
则
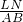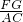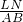=，∴++===2．分析：若将所求的等式左边进行通分，解起来会非常麻烦，所以要通过相似三角形得出的对应成比例相等来求证；根据△ADE∽△ABC、△BFG∽△BAC得出的对应成比例线段，用分母为AB的式子替换掉
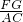、，然后再通过这些线段和AB的关系来证明所求的结论．点评：此题主要考查了平行四边形的性质以及相似三角形的判定和性质．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
ah，即三角形面积等于水平宽与铅垂高乘积的一半．
），中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高（
）”．我们可得出一种计算三角形面积的新方法：
，即三角形面积等于水平宽与铅垂高乘积的一半．
轴于点A（3，0），交
轴于点B．
；
，若存在，求出P点的坐标；若不存在，请说明理由．
ah，即三角形面积等于水平宽与铅垂高乘积的一半．