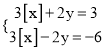题目内容
【题目】下列说法中错误的是（ ）
A. 若∠C=∠A–∠B，则△ABC为直角三角形
B. 若a∶b∶c=2∶2∶2
，则△ABC为直角三角形
C. 若a=
c，b=
c，则△ABC为直角三角形
D. 若∠A∶∠B∶∠C=3∶4∶5，则△ABC为直角三角形
【答案】D
【解析】A、若∠C=∠A-∠B，则2∠A=180°，所以∠A=90°，则△ABC为直角三角形，该说法正确；
B、若a：b：c=2：2：2
，由勾股定理的逆定理可得：a2+b2=c2，则△ABC为直角三角形，该说法正确；
C、若a=
c，b=
c，由勾股定理的逆定理可得：a2+b2=c2，则△ABC为直角三角形，该说法正确；
D、若∠A：∠B：∠C=3：4：5，则三角形中最大角为75°≠90°则△ABC不为直角三角形，该说法错误；
故选D．
【题目】某公司需招聘一名员工，对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核．甲、乙、丙各项得分如下表：
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
（1）根据三项得分的平均分，从高到低确定三名应聘者的排名顺序．
（2）该公司规定：笔试，面试、体能得分分别不得低于80分，80分，70分，并按60%，30%，10%的比例计入总分（不计其他因素条件），请你说明谁将被录用．
【题目】如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答．
（1）数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：
平面图 | a | b | c | d |
顶点数(S) | 7 | |||
边数(M) | 9 | |||
区域数(N) | 3 |
（2）根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系为 ；
（3）如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有 条边．
