题目内容
已知:OA、OB是⊙O的半径,且OA⊥OB,P是射线OA上一点(点A除外),直线BP交⊙O于点Q,过Q作⊙O的切线交直线OA与点E。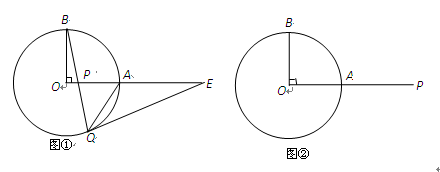
(1)如图①,若点P在线段OA上,求证:∠OBP+∠AQE=45°;(本题4分)
(2)探究:若点P在线段OA的延长线上,其它条件不变,∠OBP与∠AQE之间是否存在某种确定的等量关系?请你完成图②,并写出结论(不需要证明)。(本题3分)
(1)见解析(2)∠OBP-∠AQE=45°
解析试题分析:(1)连接OQ,∵QE是⊙O的切线,OQ是半径OQ⊥QE∴∠OQE=90°
∵OA⊥OB∴∠BOA=90°∴∠BQA=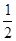 ∠BOA=45°
∠BOA=45°
∴∠OQB+∠AQE=90°-45°=45°
∵OB=OA∴∠OBP=∠OQB
∴∠OBP+∠AQE=45°
(2)∠OBP-∠AQE=45°(图形正确1分,结论正确2分)
考点:本题考查了垂径定理
点评:此类试题属于难度较大的试题,本题考查的是垂径定理在实际生活中的应用,解答此类题目的关键是根据题意画出图形,利用数形结合进行解答

练习册系列答案
相关题目

 已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.
已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.