题目内容
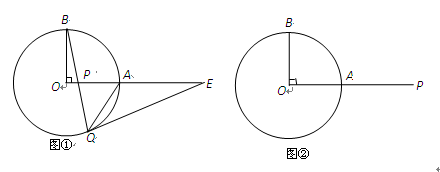
25、已知:OA、OB是⊙O的半径,且OA⊥OB,P是射线OA上一点(点A除外),直线BP交⊙O于点Q,
(1)如图①,若点P在线段OA上,PE=EQ,求证:QE是⊙O的切线;
(2)如图①,若点P在线段OA上,过Q作⊙O的切线交直线OA与点E.
①求证:∠OBP+∠AQE=45°;
②若点P在线段OA的延长线上,其它条件不变,∠OBP与∠AQE之间是否存在某种确定的等量关系?请你完成图②,并写出结论(不需要证明).过Q作⊙O的切线交直线OA于点E.

(1)如图①,若点P在线段OA上,PE=EQ,求证:QE是⊙O的切线;
(2)如图①,若点P在线段OA上,过Q作⊙O的切线交直线OA与点E.
①求证:∠OBP+∠AQE=45°;
②若点P在线段OA的延长线上,其它条件不变,∠OBP与∠AQE之间是否存在某种确定的等量关系?请你完成图②,并写出结论(不需要证明).过Q作⊙O的切线交直线OA于点E.

分析:(1)可连OQ,要证QE是⊙O的切线,通过∠OBP与∠OQP的转化,证明OQ⊥QE即可,
(2)①连接AB,则△AOB是等腰直角三角形,∠OBA=45°,由弦切角定理得,∠AQE=∠QBA,所以可求得∠OBP+∠AQE=∠OBP+∠ABP=∠OBA=45°;
②连接AB,则△AOB是等腰直角三角形,∠OBA=45°;由弦切角定理得∠AQE=∠QBA,即可求得∠OBP-∠AQE=∠OBP-∠ABP=∠OBA=45度.
(2)①连接AB,则△AOB是等腰直角三角形,∠OBA=45°,由弦切角定理得,∠AQE=∠QBA,所以可求得∠OBP+∠AQE=∠OBP+∠ABP=∠OBA=45°;
②连接AB,则△AOB是等腰直角三角形,∠OBA=45°;由弦切角定理得∠AQE=∠QBA,即可求得∠OBP-∠AQE=∠OBP-∠ABP=∠OBA=45度.
解答: 证明:(1)证明:连接OQ;
证明:(1)证明:连接OQ;
∵BO⊥OE,
∴∠BOE=90°,
∴∠OBP+∠BPO=90°;
∵PE=EQ,
∴∠EPQ=∠EQP,
∵∠EPQ=∠BPO,
∴∠EQP=∠BPO,
又∵∠OBP=∠OQP,
∴∠EQP+∠OQP=90°,
即∠OQE=90°,
∴EQ是⊙O的切线.
(2)①证明:(1)连接AB,
∵OB=OA,OB⊥OA
∴△AOB是等腰直角三角形,∠OBA=45°
∵EQ是切线
∴∠AQE=∠QBA
∴∠OBP+∠AQE=∠OBP+∠ABP=∠OBA=45°;
解:②如图,连接AB
∵OB=OA,OB⊥OA
∴△AOB是等腰直角三角形,∠OBA=45°
∵EQ是切线
∴∠AQE=∠QBA
∴∠OBP-∠AQE=∠OBP-∠ABP=∠OBA=45°.
 证明:(1)证明:连接OQ;
证明:(1)证明:连接OQ;∵BO⊥OE,
∴∠BOE=90°,
∴∠OBP+∠BPO=90°;
∵PE=EQ,
∴∠EPQ=∠EQP,
∵∠EPQ=∠BPO,
∴∠EQP=∠BPO,
又∵∠OBP=∠OQP,
∴∠EQP+∠OQP=90°,
即∠OQE=90°,
∴EQ是⊙O的切线.
(2)①证明:(1)连接AB,
∵OB=OA,OB⊥OA
∴△AOB是等腰直角三角形,∠OBA=45°
∵EQ是切线
∴∠AQE=∠QBA
∴∠OBP+∠AQE=∠OBP+∠ABP=∠OBA=45°;
解:②如图,连接AB
∵OB=OA,OB⊥OA
∴△AOB是等腰直角三角形,∠OBA=45°
∵EQ是切线
∴∠AQE=∠QBA
∴∠OBP-∠AQE=∠OBP-∠ABP=∠OBA=45°.
点评:此题主要考查了切线的判定与性质和等腰三角形的性质,根据求证的结论,使用分析推敲证明过程中所需要的条件,进而分析添加辅助线的方法,是平面几何证明必须掌握的技能,大家一定要熟练掌握,而在(2)中根据已知条件分析转化的方向也是解题的主要思想.解决就是寻找解题的思路,由已知出发,找寻转化方向和从结论出发寻找转化方向要结合在一起使用.

练习册系列答案
相关题目
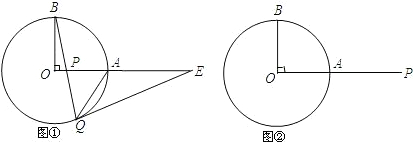
 已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.
已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.