题目内容
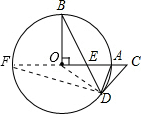
 已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.
已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.(1)求证:CE=CD;
(2)若OE=1,AE=2,求AD的长度.
分析:(1)连接OD,由DC为圆O的切线,根据切线的性质得到OD与DC垂直,可得出∠ODB+∠EDC=90°,再由OB与OA垂直,得到∠B+∠BEO=90°,由OB=OD,根据等边对等角可得∠B=∠ODB,根据等角的余角相等可得∠EDC=∠BEO,再根据对顶角相等可得∠BEO=∠CED,等量代换可得∠CED=∠CDE,根据等角对等边可得CE=CD,得证;
(2)延长AO与圆O交于点F,连接DF,由DC为圆O的切线,根据弦切角等于夹弧所对的圆周角,再加上一对公共角,利用两对对应角相等的两三角形相似可得出三角形FDC与三角形ADC相似,由OE及AE的长,利用OE+EA可得出OA的长,进而得到AF的长,设CD=x,根据第一问的结论得到CE=x,由CE-AE表示出AC,由相似得比例可列出关于x的方程,求出方程的解得到x的值,确定出AC的长,进而得到AD与FD的比值,根据比值分别设出AD=k,与FD=2k,在直角三角形AFD中,利用勾股定理得到关于k的方程,求出方程的解得到k的值,即可得出AD的长.
(2)延长AO与圆O交于点F,连接DF,由DC为圆O的切线,根据弦切角等于夹弧所对的圆周角,再加上一对公共角,利用两对对应角相等的两三角形相似可得出三角形FDC与三角形ADC相似,由OE及AE的长,利用OE+EA可得出OA的长,进而得到AF的长,设CD=x,根据第一问的结论得到CE=x,由CE-AE表示出AC,由相似得比例可列出关于x的方程,求出方程的解得到x的值,确定出AC的长,进而得到AD与FD的比值,根据比值分别设出AD=k,与FD=2k,在直角三角形AFD中,利用勾股定理得到关于k的方程,求出方程的解得到k的值,即可得出AD的长.
解答:解:(1)连接OD,如图所示:
∵DC为圆O的切线,
∴OD⊥DC,
∴∠ODC=90°,即∠ODB+∠EDC=90°,
∵OB⊥OC,∴∠BOE=90°,
∴∠B+∠BEO=90°,
又∵OB=OD,
∴∠B=∠ODB,
∴∠EDC=∠BEO,又∠BEO=∠CED,
∴∠EDC=∠CED,
∴CE=CD;
(2)延长AO与圆O交于点F,连接DF,
∵CD为圆O的切线,∠ADC为弦切角,
∴∠ADC=∠F,又∠C=∠C,
∴△ADC∽DFC,
∴
=
=
,
设CD=x,且OE=1,AE=2,
则CE=x,CA=x-2,
∴
=
,即x2=x2+2x-8,
解得:x=4,
∴AC=4-2=2,
∴
=
=
=
,
∵AF为圆O的直径,∴∠ADF=90°,
在直角三角形ADF中,
AF=2OA=2(OE+AE)=6,设AD=k,则DF=2k,
根据勾股定理得:k2+(2k)2=36,
解得:k=
,
则AD=
.

∵DC为圆O的切线,
∴OD⊥DC,
∴∠ODC=90°,即∠ODB+∠EDC=90°,
∵OB⊥OC,∴∠BOE=90°,
∴∠B+∠BEO=90°,
又∵OB=OD,
∴∠B=∠ODB,
∴∠EDC=∠BEO,又∠BEO=∠CED,
∴∠EDC=∠CED,
∴CE=CD;
(2)延长AO与圆O交于点F,连接DF,
∵CD为圆O的切线,∠ADC为弦切角,
∴∠ADC=∠F,又∠C=∠C,
∴△ADC∽DFC,
∴
| AC |
| CD |
| CD |
| CF |
| AD |
| DF |
设CD=x,且OE=1,AE=2,
则CE=x,CA=x-2,
∴
| x-2 |
| x |
| x |
| x+4 |
解得:x=4,
∴AC=4-2=2,
∴
| AD |
| DF |
| AC |
| CD |
| 2 |
| 4 |
| 1 |
| 2 |
∵AF为圆O的直径,∴∠ADF=90°,
在直角三角形ADF中,
AF=2OA=2(OE+AE)=6,设AD=k,则DF=2k,
根据勾股定理得:k2+(2k)2=36,
解得:k=
6
| ||
| 5 |
则AD=
6
| ||
| 5 |
点评:此题考查了切线的性质,等腰三角形的性质,等角的余角相等,相似三角形的判定与性质,比例的性质,以及勾股定理,利用了转化及方程的思想,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
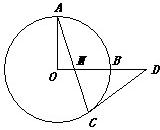 20、已知:如图,在⊙O中,OA和OB是半径,且AO⊥OB,弦AC交OB于M,在O的延长线上取一点D,使∠DCM=∠DMC.
20、已知:如图,在⊙O中,OA和OB是半径,且AO⊥OB,弦AC交OB于M,在O的延长线上取一点D,使∠DCM=∠DMC.




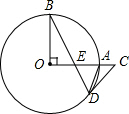 已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.
已知,OA和OB是⊙O的半径,并且OA⊥OB,E是OA上任一点,BE的延长线交⊙O于D,过D的⊙O的切线交OA的延长线于C.