题目内容
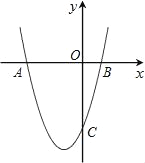
【题目】如图，抛物线y＝x2+bx+c经过点A（﹣4，0）和C点（0，﹣4），与x轴另一个交点为B．
（1）求此二次函数的解析式和顶点D的坐标；
（2）求出A、B两点之间的距离；
（3）直接写出当y＞﹣4时，x的取值范围．
【答案】（1）y＝x2+3x﹣4；D（﹣
，﹣
）；（2）5；（3）x＜﹣3或x＞0．
【解析】
（1）根据抛物线y=x2+bx+c经过点A（-4，0）和C点（0，-4），可以求得该函数的解析式，然后根据配方法即可求出该函数的顶点坐标；
（2）根据（1）中的函数解析式可以求得点B的坐标，然后根据点A的坐标，即可求得AB的长；
（3）根据题目中的函数解析式和过点C（0，-4）、二次函数的性质即可写出当y＞-4时，x的取值范围．
解：（1）∵抛物线y＝x2+bx+c经过点A（﹣4，0）和C点（0，﹣4），
∴
，得
，
即抛物线y＝x2+3x﹣4，
∵y＝x2+3x﹣4＝（x+）2﹣ ，
∴该抛物线的顶点坐标为（﹣，﹣）；
（2）令y＝0，0＝x2+3x﹣4，
解得，x1＝﹣4，x2＝1，
∴点B的坐标为（1，0），
∵点A的坐标为（﹣4，0），
∴AB＝1﹣（﹣4）＝5；
（3）∵y＝x2+3x﹣4＝（x+）2﹣，过点（0，﹣4），
∴当y＞﹣4时，x的取值范围是x＜﹣3或x＞0．
【题目】我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动，为了解学生对四种项目的喜欢情况，随机调查了该校m名学生最喜欢的一种项目（每名学生必选且只能选择四种活动项目的一种），并将调查结果绘制成如下的不完整的统计图表：
学生最喜欢的活动项目的人数统计表
项目 | 学生数（名） | 百分比 |
丢沙包 | 20 | 10% |
打篮球 | 60 | p% |
跳大绳 | n | 40% |
踢毽球 | 40 | 20% |
根据图表中提供的信息，解答下列问题：
（1）m= ，n= ，p= ；
（2）请根据以上信息直接补全条形统计图；
（3）根据抽样调查结果，请你估计该校2000名学生中有多少名学生最喜欢跳大绳．
