题目内容
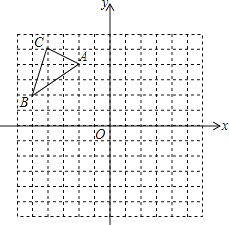
【题目】如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，以格点为顶点分别按下列要求画图：
(1)画一条线段MN,使MN=
；
(2)画△ABC,三边长分别为3,
,
.
【答案】见解析
【解析】
（1）因为正方形网格中的每个正方形边长都是1，根据勾股定理可得，直角边长为2和3的直角三角形的斜边长是
；
（2）直角边长是1和2的直角三角形的斜边长是
，直角边长是2和2的直角三角形的斜边长是
，与长是3的线段，使它们能首尾相接，可得所求三角形．
(1)因为
=，即直角边长为2和3的直角三角形的斜边长是；所以线段MN就是所求；
(2) 因为
=，即直角边长是1和2的直角三角形的斜边长是；因为
=，即直角边长是2和2的直角三角形的斜边长是，它们与长是3的线段，使它们能首尾相接，所以△ABC是所求.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某超市销售一种商品，成本每千克30元，规定每千克售价不低于成本，且不高于70元，经市场调查，每天的销售量y（千克）与每千克售价x（元）满足一次函数关系，部分数据如下表：
售价x（元/千克） | 40 | 50 | 60 |
销售量y（千克） | 100 | 80 | 60 |
（1）求y与x之间的函数表达式；
（2）设商品每天的总利润为W（元），求W与x之间的函数表达式（利润=收入成本）；
（3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少元时获得最大利润，最大利润是多少？
【题目】下表是小华同学一个学期数学成绩的记录．根据表格提供的信息，回答下列的问题：
考试类别 | 平时考试 | 期中考试 | 期末考试 | |||
第一单元 | 第二单元 | 第三单元 | 第四单元 | |||
成绩（分） | 85 | 78 | 90 | 91 | 90 | 94 |
（1）小明6次成绩的众数是 ，中位数是 ；
（2）求该同学这个同学这一学期平时成绩的平均数；
（3）总评成绩权重规定如下：平时成绩占20%，期中成绩占30%，期末成绩占50%，请计算出小华同学这一个学期的总评成绩是多少分？
