题目内容
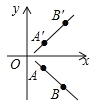
【题目】王杰同学在解决问题“已知A、B两点的坐标为A（3，﹣2）、B（6，﹣5）求直线AB关于x轴的对称直线A′B′的解析式”时，解法如下：先是建立平面直角坐标系（如图），标出A、B两点，并利用轴对称性质求出A′、B′的坐标分别为A′（3，2），B′（6，5）；然后设直线A′B′的解析式为y=kx+b（k≠0），并将A′（3，2）、B′（6，5）代入y=kx+b中，得方程组：
，解得
，最后求得直线A′B′的解析式为y=x﹣1．则在解题过程中他运用到的数学思想是（ ）
A．分类讨论与转化思想 B．分类讨论与方程思想
C．数形结合与整体思想 D．数形结合与方程思想
【答案】D．
【解析】
试题分析：第一步：建立平面直角坐标系，标出A、B两点，并利用轴对称性质求出A′、B′的坐标分别为A′（3，2），B′（6，5），这是依据轴对称的性质求得点的坐标（有序实数对），运用了数形结合的数学思想；
第二步：设直线A′B′的解析式为y=kx+b（k≠0），并将A′（3，2）、B′（6，5）代入y=kx+b中，得方程组
，解得：
，最后求得直线A′B′的解析式为y=x﹣1，这里根据一次函数图象上点的坐标特征，列出方程求得待定系数，运用了方程思想；
所以王杰同学在解题过程中，运用到的数学思想是数形结合与方程思想．故选D．
练习册系列答案
阅读快车系列答案
相关题目
