题目内容
如图,矩形 的对角线
的对角线 经过坐标原点
经过坐标原点 ,矩形
,矩形 的边分别平
的边分别平
行于坐标轴,点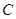 在反比例函数
在反比例函数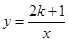 的图象上.若点
的图象上.若点 的坐标为
的坐标为 ,
,
 则
则 的值为 .
的值为 .
 的对角线
的对角线 经过坐标原点
经过坐标原点 ,矩形
,矩形 的边分别平
的边分别平
行于坐标轴,点
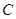 在反比例函数
在反比例函数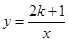 的图象上.若点
的图象上.若点 的坐标为
的坐标为 ,
, 则
则 的值为 .
的值为 .
分析:由点A的坐标为(-2,-2),矩形ABCD的边分别平行于坐标轴,可设D点坐标为(a,-2),B点坐标为(-2,b),则C点坐标为(a,b),又矩形ABCD的对角线BD经过坐标原点O,则直线BD的解析式可设为y=mx,然后把点D(a,-2),B点(-2,b)分别代入y=mx得到am=-2,-2m=b,易得ab="-"
 ?(-2m)=4,再利用点C(a,b)在反比例函数
?(-2m)=4,再利用点C(a,b)在反比例函数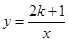 的图象上,根据反比例函数图象上点的坐标特点得到2k+1=ab=4,解方程即可得到k的值.
的图象上,根据反比例函数图象上点的坐标特点得到2k+1=ab=4,解方程即可得到k的值.解:∵点A的坐标为(-2,-2),矩形ABCD的边分别平行于坐标轴,
∴B点的横坐标为-2,D点的纵坐标为-2,
设D点坐标为(a,-2),B点坐标为(-2,b),则C点坐标为(a,b),
∵矩形ABCD的对角线BD经过坐标原点O,
∴直线BD的解析式可设为y=mx,
把点D(a,-2),B点(-2,b)分别代入y=mx得,am=-2,-2m=b,
∴a=-
 ,
,∴ab=-
 ?(-2m)=4,
?(-2m)=4,∵点C(a,b)在反比例函数
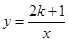 的图象上,
的图象上,∴2k+1=ab=4,
∴k=
 .
.故答案为
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

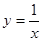
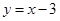
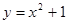
 上,则k的值是
上,则k的值是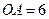 ,
,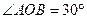 ,则经过点
,则经过点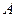 的反比例函数的解析式为
的反比例函数的解析式为
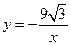
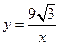
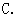

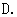
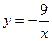
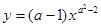 是反比例函数,则
是反比例函数,则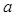 的值是( ▲ )
的值是( ▲ )
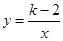 的图象如图2,则一元二次
的图象如图2,则一元二次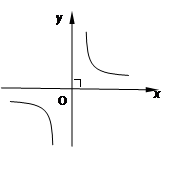
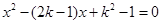 根的情况是( )
根的情况是( ) ,下列结论中不正确的是( )
,下列结论中不正确的是( ) 时,
时,
 时,
时, 随着
随着 的增大而增大
的增大而增大 图象上有三个点
图象上有三个点 ,
, ,
, ,其中
,其中 ,则
,则 ,
, ,
, 的大小关系是__________________
的大小关系是__________________