题目内容
已知：如图，在正方形ABCD中，P为对角线AC上的一动点，PE⊥AB于E，PF⊥BC于F，过点P作DP的垂线交BC于点G，DG交AC于点Q．下列说法：①EF=DP；②EF⊥DP；③| DG |
| DP |
| 2 |
| AP2+QC2 |
| PQ2 |
| 2 |
| A、①②③④ | B、①②③ |
| C、①②④ | D、①③④ |
分析：根据题意先证明△AHP≌△AEP，△PHD≌△EPF，从而得到①②正确，再由三角形PDG为等腰直角三角形，得出③正确．
解答：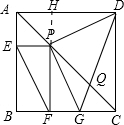
解：作PH⊥AD交AD于H，
∵PH=PE，∠HAP=∠EAP，∠AHP=∠AEP
∴△AHP≌△AEP（AAS）
∴AH=AE，HD=BE=PF，
∵HP=EP，∠EPF=∠PHD=90°
∴△PHD≌△EPF（HL）
∴EF=DP，∠EFP=∠PDH，
∵EP平行且相等于BF，BE=FP
∴△EBF≌△EPF（HL）
∴EB=PF，∠EFP=∠FPG，
∵∠EBF=∠PFG=90°，
∴∠BEF=∠EFP=∠FPG，
∴△EBF≌△PFG（ASA）
∴EP平行且相等于FG
∴四边形EFGP是平行四边形
依题意PG⊥DP，故EF⊥DP，
由上得出△PHD≌△EPF，△EBF≌△EPF，△EBF≌△PFG
∴△PHD≌△PFG
∴PD=PG，三角形PDG为等腰直角三角形，
故
=
所以①②③正确，故选B．
解：作PH⊥AD交AD于H，∵PH=PE，∠HAP=∠EAP，∠AHP=∠AEP
∴△AHP≌△AEP（AAS）
∴AH=AE，HD=BE=PF，
∵HP=EP，∠EPF=∠PHD=90°
∴△PHD≌△EPF（HL）
∴EF=DP，∠EFP=∠PDH，
∵EP平行且相等于BF，BE=FP
∴△EBF≌△EPF（HL）
∴EB=PF，∠EFP=∠FPG，
∵∠EBF=∠PFG=90°，
∴∠BEF=∠EFP=∠FPG，
∴△EBF≌△PFG（ASA）
∴EP平行且相等于FG
∴四边形EFGP是平行四边形
依题意PG⊥DP，故EF⊥DP，
由上得出△PHD≌△EPF，△EBF≌△EPF，△EBF≌△PFG
∴△PHD≌△PFG
∴PD=PG，三角形PDG为等腰直角三角形，
故
| DG |
| DP |
| 2 |
所以①②③正确，故选B．
点评：本题综合考查了全等三角形的判定，正方形的性质，矩形的性质等有关知识的运用，涉及大量的全等三角形的证明．
练习册系列答案
海淀黄冈名师导航系列答案
相关题目
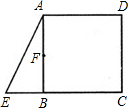已知：如图，在正方形ABCD中，E是CB延长线上一点，EB=
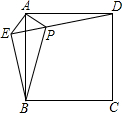已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
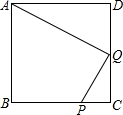已知：如图，在正方形ABCD中，P是BC上的点，且BP=3PC，Q是CD的中点．△ADQ与△QCP是否相似？
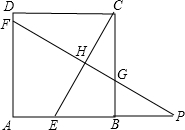、CE、CB于点F、H、G，交AB的延长线于点P．
已知：如图，在正方形ABCD中，E、F分别是AD、CD的中点．