题目内容
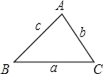
【题目】在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示.
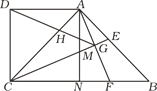
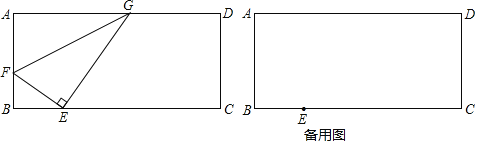
(1)如图,在△ABC中,∠A=2∠B,且∠A=60度.求证:a2=b(b+c).

(2)如果一个三角形的一个内角等于另一个内角的2倍,我们称这样的三角形为“倍角三角形”.第一问中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?并证明你的结论.
(3)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数.
【答案】(1)见解析;(2)成立,证明见解析;(3)边长为4,5,6的三角形
【解析】
(1)由A=2∠B,∠A=60°,得∠B=30°,∠C=90°,结合含30°角的直角三角形三边长的比例关系,即可得到答案;
(2)延长BA至点D,使AD=AC=b,连接CD,易证ACD,BCD是等腰三角形,CD=BC=a,AC=AD=b,BD=b+c,易证ACD~CBD,得![]() ,进而即可得到结论;
,进而即可得到结论;
(3)由题意得:若△ABC是倍角三角形,由∠A=2∠B,则a2=b(b+c),且a>b,然后分情况讨论:当a>c>b时,当c>a>b时,当a>b>c时,分别求出符合要求的值,即可.
(1)∵∠A=2∠B,∠A=60°,
∴∠B=30°,∠C=90°,
∴c=2b,a=![]() b,
b,
∴a2=3b2=b(b+c);
(2)关系式a2=b(b+c)仍然成立,理由如下:
延长BA至点D,使AD=AC=b,连接CD,则ACD是等腰三角形,
∴∠ACD=∠D,
∵∠BAC是ACD的一个外角,
∴∠BAC=∠D+∠ACD=2∠D,
∵∠BAC=2∠B,
∴∠B=∠D,
∴CD=BC=a,∠B=∠ACD,
∴BD=AB+AD=b+c,
又∵∠D=∠D,
∴ACD~CBD,
∴![]() ,即:
,即:![]() ,
,
∴a2=b(b+c);
(3)若△ABC是倍角三角形,由∠A=2∠B,则a2=b(b+c),且a>b.
①当a>c>b时,设a=n+1,c=n,b=n﹣1,(n为大于1的正整数),
代入a2=b(b+c),得(n+1)2=(n﹣1)(2n﹣1),解得:n=5,
∴a=6,b=4,c=5,
②当c>a>b及a>b>c时,
均不存在三条边长恰为三个连续正整数的倍角三角形.
综上所述:边长为4,5,6的三角形即为所求倍角三角形.