Ő‚ńŅńŕ»›
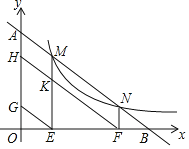
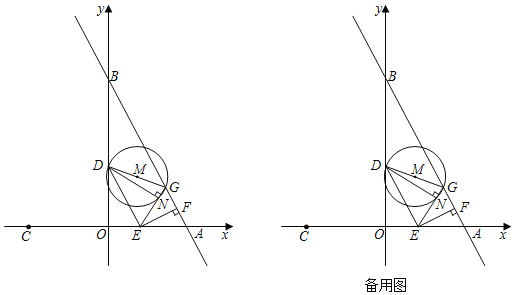
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy£Ĺ©Ā2x+6”Žx÷Š£¨y÷Š∑÷ĪūĹĽA£¨BŃĹĶ„£¨Ķ„AĻō”ŕ‘≠Ķ„OĶń∂‘≥∆Ķ„ «Ķ„C£¨∂ĮĶ„Eī”A≥Ų∑Ę“‘√Ņ√Ž1łŲĶ•őĽĶńňŔ∂»‘ň∂ĮĶĹĶ„C£¨Ķ„D‘ŕŌŖ∂őOB…Ō¬ķ◊„tan°ŌDEO£Ĺ2£¨ĻżEĶ„◊ųEF°ÕAB”ŕĶ„F£¨Ķ„AĻō”ŕĶ„FĶń∂‘≥∆Ķ„ő™Ķ„G£¨“‘DGő™÷Īĺ∂◊ų°—M£¨…ŤĶ„E‘ň∂ĮĶń Īľšő™t√Ž£Ľ
£®1£©ĶĪĶ„E‘ŕŌŖ∂őOA…Ō‘ň∂Į£¨t£Ĺ°°°° Ī£¨°ųAEF”Ž°ųEDOĶńŌŗň∆Ī»ő™1£ļ![]() £Ľ
£Ľ
£®2£©ĶĪ°—M”Žy÷ŠŌŗ«– Ī£¨«ůtĶń÷Ķ£Ľ
£®3£©»Ű÷ĪŌŖEG”Ž°—MĹĽ”ŕĶ„N£¨ «∑Ůīś‘ŕt ĻNG£Ĺ![]() £¨»Űīś‘ŕ£¨«ů≥ŲtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
£¨»Űīś‘ŕ£¨«ů≥ŲtĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨ňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©t£Ĺ
£Ľ£®2£©t£Ĺ![]() ĽÚ5£Ľ£®3£©īś‘ŕ£¨t£Ĺ
ĽÚ5£Ľ£®3£©īś‘ŕ£¨t£Ĺ![]() ĽÚ
ĽÚ![]() ĽÚ
ĽÚ![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©Ō»«ů÷ĪŌŖ”Ž◊ÝĪÍ÷ŠĶńĹĽĶ„◊ÝĪÍ£¨‘Ŕ÷§°ųAEF°◊°ųEDO°◊°ųABO£¨”…°ųAEF”Ž°ųEDOĶńŌŗň∆Ī»ő™1£ļ![]() £¨ľīŅ…«ůĶ√tĶń÷Ķ£Ľ
£¨ľīŅ…«ůĶ√tĶń÷Ķ£Ľ
£®2£©”…°—M”Žy÷ŠŌŗ«–Ņ…÷™£ļDG°Õy÷Š£¨∑÷ŃĹ÷÷«ťŅŲ£ļ0°‹t°‹3ĽÚ3£ľt°‹6£¨∑÷Īū”…D°ĘGĶń◊›◊ÝĪÍŌŗĶ»Ĺ®ŃĘ∑Ĺ≥Ő«ůĹ‚ľīŅ…£Ľ
£®3£©∑÷»ż÷÷«ťŅŲ£ļ0°‹t°‹![]() ĽÚ
ĽÚ![]() £ľt°‹3ĽÚ3£ľt°‹6£¨∑÷ĪūĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚ľīŅ…£ģ
£ľt°‹3ĽÚ3£ľt°‹6£¨∑÷ĪūĹ®ŃĘ∑Ĺ≥Ő«ůĹ‚ľīŅ…£ģ
Ĺ‚£ļ£®1£©‘ŕy£Ĺ©Ā2x+6÷–£¨ŃÓx£Ĺ0£¨Ķ√£ļy£Ĺ6£¨
ŃÓy£Ĺ0£¨Ķ√£ļ©Ā2x+6£Ĺ0£¨
Ĺ‚Ķ√£ļx£Ĺ3£¨
°ŗA£®3£¨0£©£¨B£®0£¨6£©£¨C£®©Ā3£¨0£©
°ŗOA£Ĺ3£¨OB£Ĺ6£¨AB£Ĺ3![]() £¨AE£Ĺt£¨OE£Ĺ3©Āt£¨
£¨AE£Ĺt£¨OE£Ĺ3©Āt£¨
°ŗtan°ŌBAO£Ĺ![]() £Ĺ2
£Ĺ2
°Ŗtan°ŌDEO£Ĺ2
°ŗ°ŌBAO£Ĺ°ŌDEO
°ŖEF°ÕAB
°ŗ°ŌAFE£Ĺ°ŌDOE£Ĺ90°„
°ŗ°ųAEF°◊°ųEDO°◊°ųABO
![]() £¨ľī
£¨ľī![]()
°ŗAF£Ĺ![]() t£Ľ
t£Ľ
°Ŗ°ųAEF”Ž°ųEDOĶńŌŗň∆Ī»ő™1£ļ![]() £¨
£¨
°ŗ![]() £¨ľīOE£Ĺ
£¨ľīOE£Ĺ![]() AF
AF
°ŗ3©Āt£Ĺ![]() °Ń
°Ń![]() t£¨
t£¨
Ĺ‚Ķ√£ļt£Ĺ![]() £Ľ
£Ľ
Ļ īūįłő™£ļt£Ĺ![]() £Ľ
£Ľ
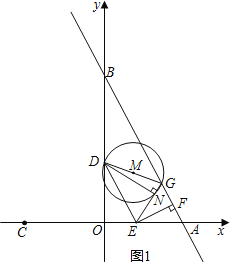
£®2£©°Ŗ°—M”Žy÷ŠŌŗ«–
°ŗDG°Õy÷Š
ĶĪ0°‹t°‹3 Ī£¨![]()
°Ŗtan°ŌDEO£Ĺ2
°ŗ![]()
°ŗ![]()
°Ŗ![]() £¨°ųAEF°◊°ųABO
£¨°ųAEF°◊°ųABO
°ŗ![]()
°ŗ![]()
°ŖĶ„A°ĘGĻō”ŕĶ„F∂‘≥∆
°ŗ![]()
°ŗ![]()
Ĺę![]() īķ»Ž
īķ»Ž![]() ÷–£¨Ķ√£¨
÷–£¨Ķ√£¨![]()
Ĺ‚Ķ√![]() £¨
£¨
°ŗG£®3©Ā![]() t£¨
t£¨![]() t£©£¨D£®0£¨6©Ā2t£©£¨
t£©£¨D£®0£¨6©Ā2t£©£¨
°ŗ![]() t£Ĺ6©Ā2t£¨Ĺ‚Ķ√£ļt£Ĺ
t£Ĺ6©Ā2t£¨Ĺ‚Ķ√£ļt£Ĺ![]() £Ľ
£Ľ
ĶĪ3£ľt°‹6 Ī£¨Õ¨ņŪĶ√G£®3©Ā![]() t£¨
t£¨![]() t£©£¨D£®0£¨2t©Ā6£©£¨
t£©£¨D£®0£¨2t©Ā6£©£¨
°ŗ![]() t£Ĺ2t©Ā6£¨Ĺ‚Ķ√£ļt£Ĺ5£¨
t£Ĺ2t©Ā6£¨Ĺ‚Ķ√£ļt£Ĺ5£¨
◊Ř…Ōňý Ų£¨ĶĪ°—M”Žy÷ŠŌŗ«– Ī£¨t£Ĺ![]() ĽÚ5£Ľ
ĽÚ5£Ľ
£®3£©īś‘ŕ£ģ
ĶĪ0°‹t°‹![]() Ī£¨G£®3©Ā
Ī£¨G£®3©Ā![]() t£¨
t£¨![]() t£©£¨D£®0£¨6©Ā2t£©£¨
t£©£¨D£®0£¨6©Ā2t£©£¨
°ŖĶ„AĻō”ŕĶ„FĶń∂‘≥∆Ķ„ő™Ķ„G£¨EF°ÕAB
°ŗEG£ĹEA£Ĺt
°Ŗ°ŌOEG£Ĺ°ŌOAB+°ŌEGA£Ĺ2°ŌOAB£¨°ŌOED£Ĺ°ŌOAB
°ŗ°ŌGED£Ĺ°ŌOED£Ĺ°ŌOAB
°ŖDGő™÷Īĺ∂
°ŗ°ŌDNG£Ĺ°ŌDNE£Ĺ°ŌDOE£Ĺ90°„£¨DE£ĹDE
°ŗ°ųDEN°’°ųDEO£®AAS£©
°ŗEN£ĹOE£Ĺ3©Āt£¨NG£ĹEN©ĀEG£Ĺ3©Āt©Āt£Ĺ3©Ā2t£¨
°ŗ3©Ā2t£Ĺ![]() £¨
£¨
Ĺ‚Ķ√£ļt£Ĺ![]() £¨
£¨
ĶĪ![]() £ľt°‹3 Ī£¨NG£ĹEG©ĀEN£Ĺt©Ā£®3©Āt£©£Ĺ2t©Ā3
£ľt°‹3 Ī£¨NG£ĹEG©ĀEN£Ĺt©Ā£®3©Āt£©£Ĺ2t©Ā3
°ŗ2t©Ā3£Ĺ![]() £¨
£¨
Ĺ‚Ķ√£ļt£Ĺ![]() £Ľ
£Ľ
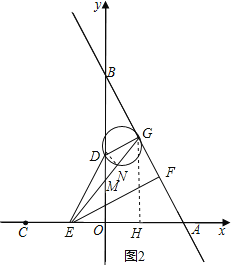
ĶĪ3£ľt°‹6 Ī£¨»ÁÕľ2£¨Ń¨Ĺ”DN£¨ĻżG◊ųGH°Õx÷Š”ŕH£¨
°ŖDG «÷Īĺ∂£¨
°ŗ°ŌDNG£Ĺ°ŌDNE£Ĺ90°„£¨
°Ŗ°ŌDMN£Ĺ°ŌEMO
°ŗ°ųDMN°◊°ųEMO
°ŗ°ŌMDN£Ĺ°ŌOEM
°ŖGH°őy÷Š
°ŗ![]() £¨ľī
£¨ľī![]() £¨
£¨
”…£®2£©Ķ√![]() £¨
£¨
°Ŗ![]() ÷Š£¨
÷Š£¨
°ŗ![]() £¨
£¨![]() £¨
£¨
°ŗ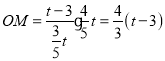 £¨
£¨
°ŗDM£ĹOD©ĀOM£Ĺ2£®t©Ā3£©©Ā![]() £®t©Ā3£©£Ĺ
£®t©Ā3£©£Ĺ![]() £®t©Ā3£©
£®t©Ā3£©
°Ŗtan°ŌOEM£Ĺ![]()
°ŗEM£Ĺ![]() OE£Ĺ
OE£Ĺ![]() £®t©Ā3£©£¨
£®t©Ā3£©£¨
°ŗsin°ŌOEM£Ĺ![]() £Ĺ
£Ĺ![]() £Ĺsin°ŌMDN£Ĺ
£Ĺsin°ŌMDN£Ĺ![]()
°ŗMN£Ĺ![]() °Ń
°Ń![]() £®t©Ā3£©£Ĺ
£®t©Ā3£©£Ĺ![]() £®t©Ā3£©
£®t©Ā3£©
°ŗNG£ĹEG©ĀEM©ĀMN£Ĺt©Ā![]() £®t©Ā3£©©Ā
£®t©Ā3£©©Ā![]() £®t©Ā3£©£Ĺ
£®t©Ā3£©£Ĺ![]() ©Ā
©Ā![]() t£¨
t£¨
°ŗ![]() £¨
£¨
Ĺ‚Ķ√£ļt£Ĺ![]() £Ľ
£Ľ
◊Ř…Ōňý Ų£¨t£Ĺ![]() ĽÚ
ĽÚ![]() ĽÚ
ĽÚ![]() £ģ
£ģ

 ľ§ĽÓňľő¨”Ňľ”ŅőŐ√ŌĶŃ–īūįł
ľ§ĽÓňľő¨”Ňľ”ŅőŐ√ŌĶŃ–īūįł ĽÓѶ ‘ĺŪŌĶŃ–īūįł
ĽÓѶ ‘ĺŪŌĶŃ–īūįł ŅőŅő”Ňń‹Ń¶Ňŗ”Ň100∑÷ŌĶŃ–īūįł
ŅőŅő”Ňń‹Ń¶Ňŗ”Ň100∑÷ŌĶŃ–īūįł