题目内容
22、如图所示，在等腰梯形ABCD中，AB∥CD，DC=AD=BC，且对角线AC垂直于腰BC，求这个梯形各内角的度数．分析：因为是等腰梯形，所以∠DAB=∠B，作CE∥AD，根据垂直及边相等，在△ABC中，可求∠CAB的大小，进而求出各个内角．
解答：解：如图所示，过点C作CE∥AD
∵DC=AD=BC，∴∠EAC=∠ECA，∠CEB=∠B，
∵∠B+∠CAB=90°，即3∠CAE=90°
∴∠CAE=30°
∴∠B=60°=∠DAB
∠D=∠DCB=120°．
∵DC=AD=BC，∴∠EAC=∠ECA，∠CEB=∠B，∵∠B+∠CAB=90°，即3∠CAE=90°
∴∠CAE=30°
∴∠B=60°=∠DAB
∠D=∠DCB=120°．
点评：熟练掌握等腰三角形的性质，能够通过作辅助线以及勾股定理找出角之间的内在联系，建立等效关系，最终得出结论．
练习册系列答案
阅读快车系列答案
相关题目
25、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，点P为BC边上任意一点，且
1、如图所示，在等腰梯形ABCD中，AD∥BC，DE⊥BC于点E，BF⊥AE于点F，请你添加一个条件，使△ABF≌△CDE．
48、如图所示，在等腰梯形ABCD中，AD∥BC，AB=CD，DE⊥BC于E，BF⊥AE于F，AE=BE．请你判断线段BF与图形中哪条线段相等，先写出你的猜想，再加以证明．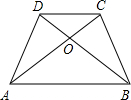
如图所示，在等腰梯形ABCD中，AB∥CD，若AB+CD=4，并且∠AOB=120°，则该等腰梯形的面积为
如图所示，在等腰梯形ABCD中，AD∥BC，过A作腰CD的平行线，AE∥CD，AB=AD=DC，∠B=60°