题目内容
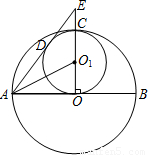
 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.
如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.(1)试探究CD与AO1的位置关系,并说明理由;
(2)若DE=4,CE=2,求AD的长.
分析:(1)连接OD,根据直径所对的圆周角是直角,以及切线长定理即可证得AO1与CD都与OD垂直,即可证得CD∥AD;
(2)根据切割线定理即可求得OE的长,进而求得半径OC的长,再依据切线长定理即可求解.
(2)根据切割线定理即可求得OE的长,进而求得半径OC的长,再依据切线长定理即可求解.
解答:解: (1)CD∥AD
(1)CD∥AD
证明:∵OC是⊙O1的直径,
∴∠ODC=90°
∵AD,AO是⊙O1的切线,
∴AO1⊥OD,
∴CD∥AD
(2)∵DE是⊙O1的切线,
∴DE2=EC•EO,即16=2EO,
∴EO=8,
∴OC=OE-EC=8-2=6.
∴AD=AO=OC=6.
 (1)CD∥AD
(1)CD∥AD证明:∵OC是⊙O1的直径,
∴∠ODC=90°
∵AD,AO是⊙O1的切线,
∴AO1⊥OD,
∴CD∥AD
(2)∵DE是⊙O1的切线,
∴DE2=EC•EO,即16=2EO,
∴EO=8,
∴OC=OE-EC=8-2=6.
∴AD=AO=OC=6.
点评:本题考查了圆周角定理,切线长定理,切割线定理,关键是证明:AO1与CD都与OD垂直.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
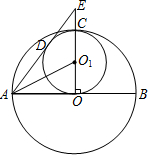 如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1=
如图,大圆O的半径OC是小圆O1的直径,且有OC垂直于圆O的直径AB.圆O1的切线AD交OC的延长线于点E,切点为D.已知圆O1的半径为r,则AO1= 4、如图,大圆O1的半径是小圆O2的半径的2倍,固定大圆,让小圆在大圆外绕大圆作无滑动滚动一周,则小圆上一点P绕小圆圆心O2自转了( )
4、如图,大圆O1的半径是小圆O2的半径的2倍,固定大圆,让小圆在大圆外绕大圆作无滑动滚动一周,则小圆上一点P绕小圆圆心O2自转了( )