题目内容
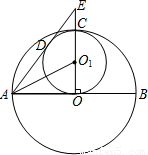
（2008•杭州）如图，大圆O的半径OC是小圆O1的直径，且有OC垂直于圆O的直径AB．圆O1的切线AD交OC的延长线于点E，切点为D．已知圆O1的半径为r，则AO1= ，DE= ．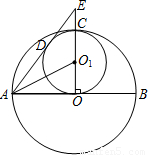
【答案】分析：连接O1D，由切线的性质知O1D⊥AE，由题意知，CO=AO=2r，O1D=O1C=r，进而由切线长定理知，AD=AO=2r；再根据勾股定理得AE2=AO2+OE2，O1E2=O1D2+DE2，然后即可得到关于DE，CE，的方程组，解之即可得到DE=
r．
解答：
解：如图，连接O1D．
∵圆O1的切线AD交OC的延长线于点E，
∴O1D⊥AE，
由题意知，CO=AO=2r，O1D=O1C=r，
由切线长定理知，AD=AO=2r，
∴AO1=
r，
由勾股定理得，AE2=AO2+OE2，
即（2r+DE）2=（2r）2+（2r+EC）2，①
O1E2=O1D2+DE2，
即（r+EC）2=r2+DE2，②
由①②解得，DE=
r．
故填空答案：
r；
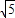r．
点评：本题利用了切线的性质，切线长定理，勾股定理等知识求解．
r．解答：
解：如图，连接O1D．∵圆O1的切线AD交OC的延长线于点E，
∴O1D⊥AE，
由题意知，CO=AO=2r，O1D=O1C=r，
由切线长定理知，AD=AO=2r，
∴AO1=
r，由勾股定理得，AE2=AO2+OE2，
即（2r+DE）2=（2r）2+（2r+EC）2，①
O1E2=O1D2+DE2，
即（r+EC）2=r2+DE2，②
由①②解得，DE=
r．故填空答案：
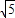r；r．点评：本题利用了切线的性质，切线长定理，勾股定理等知识求解．
练习册系列答案
相关题目
∠β．（只须作出正确图形，保留作图痕迹，不必写出作法）
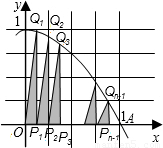
，S2=
，…；记W=S1+S2+…+Sn-1，当n越来越大时，你猜想W最接近的常数是（ ）
