题目内容
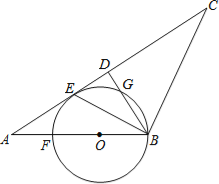
【题目】如图1,△ABC中,CA=CB,∠ACB=120°,点E、F在AB上,且∠ECF=60°.
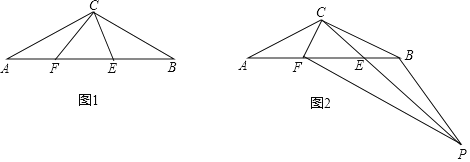
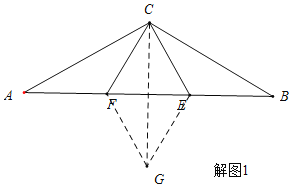
(1)①在图1中画出;点A关于直线CF的对称点G;②若EF=AF,求证:BE=EF;
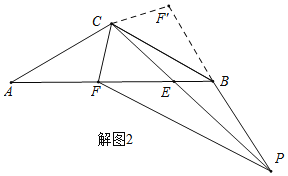
(2)如图2,∠ABP=120°,射线BP交CE的延长线于点P,求证:PB+AF=PF.
【答案】(1)①见解析,②见解析;(2)见解析.
【解析】
(1)根据对称的性质画出点G,根据对称的性质和全等三角形的性质可求证BE=EF.(2)将△ACF绕C点逆时针旋转至AC与BC重合,根据全等三角形的性质可求证PB+AF=PF.
解:(1)①如解图(1):G为点A关于直线CF的对称点;
②连接FG、CG、EG,
∵G为点A关于直线CF的对称点;
∴△ACF≌△GCF,
∴AC=CG,∠ACF=∠GCF,∠FGC=∠A.
又∵AC=BC,
∴CG=CB,
∵∠ACB=120°,∠ECF=60°,
∴∠ECG=60°﹣∠GCF=60°﹣∠ACF,∠BCE=60°﹣∠ACF,
∴∠ECG=∠ECB,
在△GCE和△BCE中
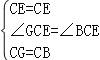
∴△GCE≌△BCE(SAS),
∴EG=BE,∠B=∠EGC,
∵∠ACB=120°,
∴∠A+∠B=60°,
∴∠EGC+∠FGC=60°,
又∵AF=EF=FG,
∴△FEG为等边三角形,
∴EF=EG=BE,即BE=EF.
(2)证明:由AC=BC,∠ACB=120°,故可将△ACF绕C点逆时针旋转120°到△BCF′位置,如解图2,
∵△ACF≌△BCF′,
∴∠A=∠CBA=∠CBF′=30°,AF=BF’,∠ACF=∠BCF′
又∵∠FBP=120°,
∴∠FBP+∠ABC+∠CBF′=180°,
∴B、P、F′在同一直线上,
又∵∠ACF+∠BCE=∠BCF′+∠BCE=60°,即∠PCF’=60°.
在△CFP和△CF′P中,
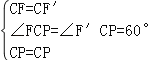 ,
,
∴△CFP≌△CF′P(SAS)
∴FP=F′P,
∵PB+BF′=BP+AF,
∴PB+AF=PF

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案