题目内容
【题目】已如抛物线y=ax2+bx+c与直线y=mx+n相交于两点,这两点的坐标分别是(0,﹣![]() )和(m﹣b,m2﹣mb+n),其中a,b,c,m,n为实数,且a,m不为0.
)和(m﹣b,m2﹣mb+n),其中a,b,c,m,n为实数,且a,m不为0.
(1)求c的值;
(2)求证:抛物线y=ax2+bx+c与x轴有两个交点;
(3)当﹣1≤x≤1时,设抛物线y=ax2+bx+c与x轴距离最大的点为P(x0,y0),求这时|y0|的最小值.
【答案】(1)c=![]() ;(2)见解析;(3)当b=0,x0=0时,这时|yo|取最小值,为|yo|=
;(2)见解析;(3)当b=0,x0=0时,这时|yo|取最小值,为|yo|=![]()
【解析】
(1)将(0,![]() )代入抛物线y=ax2+bx+c中即可;
)代入抛物线y=ax2+bx+c中即可;
(2)先求n的值,再将点的坐标(m-b,m2-mb+n)代入y=ax2+bx+c中,计算△>0即可;
(3)先根据公式分别求抛物线的对称轴和最小值,分四种情况进行讨论:
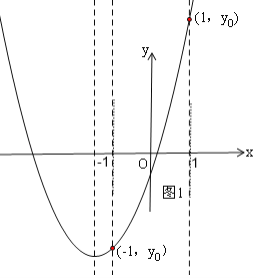
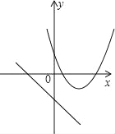
①当![]() <-1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),在x轴下方与x轴距离最大的点是(-1,yo),代入抛物线的解析式中分别求|H|和|h|,作判断即可;
<-1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),在x轴下方与x轴距离最大的点是(-1,yo),代入抛物线的解析式中分别求|H|和|h|,作判断即可;
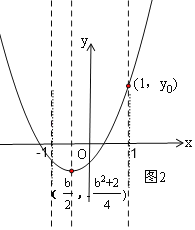
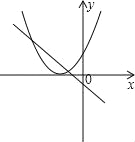
②当-1≤![]() ≤0,即0≤b≤2时,如图2,
≤0,即0≤b≤2时,如图2,
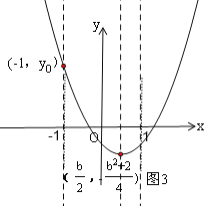
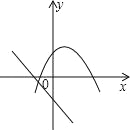
③当0<![]() ≤1,即-2≤b<0时,如图3,
≤1,即-2≤b<0时,如图3,
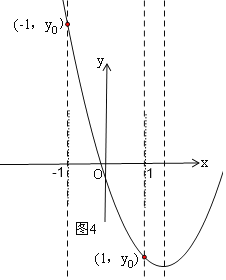
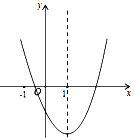
④当1<![]() ,即b<-2时,如图4,
,即b<-2时,如图4,
根据图象分别求其y0的取值范围,可得结论.
解:(1)∵(0,![]() )在y=ax2+bx+c上,
)在y=ax2+bx+c上,
∴![]() =a×02+b×0+c,
=a×02+b×0+c,
∴c=![]() ;
;
(2)又可得 n=![]() ,
,
∵点(m﹣b,m2﹣mb+n)在y=ax2+bx+c上,
∴m2﹣mb![]() =a(m﹣b)2+b(m﹣b)
=a(m﹣b)2+b(m﹣b)![]() ,
,
∴(a﹣1)(m﹣b)2=0,
若(m﹣b)=0,则(m﹣b,m2﹣mb+n)与(0,![]() )重合,与题意不合,
)重合,与题意不合,
∴a=1,
∴抛物线y=ax2+bx+c,就是y=x2+bx﹣![]() ,
,
△=b2﹣4ac=b2﹣4×(![]() )=b2+2>0,
)=b2+2>0,
∴抛物线y=ax2+bx+c与x轴有两个交点;
(3)抛物线y=x2+bx![]() 的对称轴为
的对称轴为![]() ,最小值为
,最小值为![]() ,
,
设抛物线y=x2+bx![]() 在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h,
在x轴上方与x轴距离最大的点的纵坐标为H,在x轴下方与x轴距离最大的点的纵坐标为h,
①当![]() <﹣1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),
<﹣1,即b>2时,如图1,在x轴上方与x轴距离最大的点是(1,yo),
∴|H|=yo=![]() +b>
+b>![]() ,
,
在x轴下方与x轴距离最大的点是(﹣1,yo),
∴|h|=|yo|=|![]() ﹣b|=b﹣
﹣b|=b﹣![]() >
>![]() ,
,
∴|H|>|h|,
∴这时|yo|的最小值大于![]() ;
;
②当﹣1≤![]() ≤0,即0≤b≤2时,如图2,在x轴上方与x轴距离最大的点是(1,yo),
≤0,即0≤b≤2时,如图2,在x轴上方与x轴距离最大的点是(1,yo),
∴|H|=yo=![]() +b≥
+b≥![]() ,当b=0时等号成立.
,当b=0时等号成立.
在x轴下方与x轴距离最大的点是![]() ,
,
∴|h|=|![]() |=
|=![]() ≥
≥![]() ,当b=0时等号成立.
,当b=0时等号成立.
∴这时|yo|的最小值等于![]() .
.
③当0<![]() ≤1,即﹣2≤b<0时,如图3,在x轴上方与x轴距离最大的点是
≤1,即﹣2≤b<0时,如图3,在x轴上方与x轴距离最大的点是
(﹣1,yo),
∴|H|=yo=1+(﹣1)b﹣![]() =
=![]() ﹣b>
﹣b>![]() ,在x轴下方与x轴距离最大的点是
,在x轴下方与x轴距离最大的点是 ![]() ,
,
∴|h|=|yo|=|![]() |=
|=![]() >
>![]() .
.
∴这 时|yo|的 最 小 值 大 于![]() .
.
④当1<![]() ,即b<﹣2时,如图4,在x轴上方与x轴距离最大的点是(﹣1,yo),
,即b<﹣2时,如图4,在x轴上方与x轴距离最大的点是(﹣1,yo),
∴|H|=![]() ﹣b>
﹣b>![]() ,在x轴下方与x轴距离最大的点是(1,yo),
,在x轴下方与x轴距离最大的点是(1,yo),
∴|h|=|![]() +b|=﹣(b+
+b|=﹣(b+![]() )>
)>![]() ,
,
∴|H|>|h|,
∴这时|yo|的最小值大于![]() ,
,
综上所述,当b=0,x0=0时,这时|yo|取最小值,为|yo|=![]() .
.