题目内容
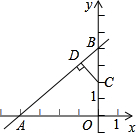 一次函数y=x+4的图象与x轴,y轴的交点分别为A、B,若C为OB的中点,则点C到直线AB的距离CD等于
一次函数y=x+4的图象与x轴,y轴的交点分别为A、B,若C为OB的中点,则点C到直线AB的距离CD等于
- A.1
- B.

- C.

- D.
B
分析:根据直线解析式可以求出OA、OB的长度,可以得出△AOB是等腰直角三角形,CD⊥AB,可以得到△BDC是等腰直角三角形,根据勾股定理可以求出CD的值.
解答:当x=0时,
y=4,
当y=0时
0=x+4
x=-4
∵函数y=x+4的图象与x轴,y轴的交点分别为A、B
∴A(-4,0),B(0,4)
∴OB=4,OA=4
∵∠AOB=90°
∴∠ABC=∠BAO=45°
∵C为OB的中点
∴BC= OB=2
OB=2
∵DC⊥AB
∴∠BDC=90°
∴∠DCB=45°
∴∠DCB=∠=DBC
∴BD=DC
在Rt△DBC中由勾股定理得
BD2+DC2=BC2
∴2CD2=22
CD= .
.
故选B.
点评:本题考查了一次函数的图象与坐标轴围成的三角形之间的关系,等腰直角三角形的性质,勾股定理得的运用.
分析:根据直线解析式可以求出OA、OB的长度,可以得出△AOB是等腰直角三角形,CD⊥AB,可以得到△BDC是等腰直角三角形,根据勾股定理可以求出CD的值.
解答:当x=0时,
y=4,
当y=0时
0=x+4
x=-4
∵函数y=x+4的图象与x轴,y轴的交点分别为A、B
∴A(-4,0),B(0,4)
∴OB=4,OA=4
∵∠AOB=90°
∴∠ABC=∠BAO=45°
∵C为OB的中点
∴BC=
 OB=2
OB=2∵DC⊥AB
∴∠BDC=90°
∴∠DCB=45°
∴∠DCB=∠=DBC
∴BD=DC
在Rt△DBC中由勾股定理得
BD2+DC2=BC2
∴2CD2=22
CD=
 .
.故选B.
点评:本题考查了一次函数的图象与坐标轴围成的三角形之间的关系,等腰直角三角形的性质,勾股定理得的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
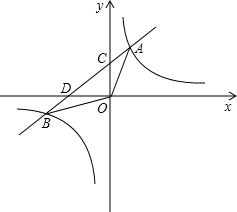 ,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO=
,与y轴交于点C,与x轴交于点D,点D的坐标为(-2,0),点A的横坐标是2,tan∠CDO=