题目内容
已知反比例函数y1=| k |
| x |
| 1 |
| 2 |
(1)求平移后的一次函数的解析式;
(2)若反比列函数y1=
| k |
| x |
(3)问当x在什么范围时y1>y2;
(4)求△CDB的面积.
分析:(1)设平移后的一次函数关系式为y=x+b根据已知的点的坐标,代入函数关系式中,即可得处于函数式;将点B的坐标代入关系式中,可得出m的值,代入一次函数式中,可得到k,即可得出平移后的一次函数关系式;
(2)由可得出反比例函数的关系式,联立两方程即可得出C、D的坐标;
(3)根据函数图象,即可求得答案;
(4)已知三点的坐标,利用两点间的距离公式,得出其中一边;再利用点到直线的距离,得出对应边上的高,代入三角形的面积公式即可得出△CDB的面积.
(2)由可得出反比例函数的关系式,联立两方程即可得出C、D的坐标;
(3)根据函数图象,即可求得答案;
(4)已知三点的坐标,利用两点间的距离公式,得出其中一边;再利用点到直线的距离,得出对应边上的高,代入三角形的面积公式即可得出△CDB的面积.
解答:解:(1)设平移后的一次函数关系式为y=x+b;
根据题意,知反比例函数y1=
的图象经过点A(4,
),
即有
=
,即k=2,
即有y1=
,
将B(2,m)代入上述关系式中,
可得m=1,
即B(2,1),代入y=x+b中,
得b=-1
即平移后的一次函数关系式为y=x-1;
(2)根据题意,
,
解之得x1=1,y1=2,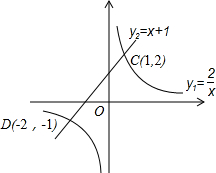
x2=-2,y2=-1,
即C(1,2)、D(-2,-1);
(3)如图:当x<-2或0<x<1时,y1>y2;
(4)有上可知点B(2,1)、C(1,2)、D(-2,-1),
即有CD=3
,
又∵点B到一次函数y2=x+1的距离d=
,
即S△CDB=
CD•d=3.
根据题意,知反比例函数y1=
| k |
| x |
| 1 |
| 2 |
即有
| 1 |
| 2 |
| k |
| 4 |
即有y1=
| 2 |
| x |
将B(2,m)代入上述关系式中,
可得m=1,
即B(2,1),代入y=x+b中,
得b=-1
即平移后的一次函数关系式为y=x-1;
(2)根据题意,
|
解之得x1=1,y1=2,
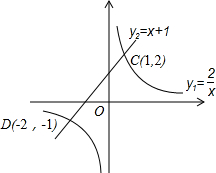
x2=-2,y2=-1,
即C(1,2)、D(-2,-1);
(3)如图:当x<-2或0<x<1时,y1>y2;
(4)有上可知点B(2,1)、C(1,2)、D(-2,-1),
即有CD=3
| 2 |
又∵点B到一次函数y2=x+1的距离d=
| 2 |
即S△CDB=
| 1 |
| 2 |
点评:本题主要考查待定系数法求函数解析式和函数交点坐标的求法,先利用反比例函数解析式求出m的值是解本题的关键;本题涉及知识点较多,难度稍大,综合性较强,要注意对各个知识点的灵活应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
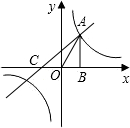 为1.过点A作AB⊥x轴于点B,△AOB的面积1.
为1.过点A作AB⊥x轴于点B,△AOB的面积1.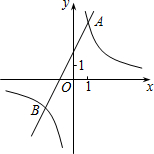 已知反比例函数y1=
已知反比例函数y1= 如图,已知反比例函数
如图,已知反比例函数 已知反比例函数
已知反比例函数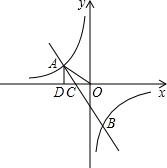 的横坐标为
的横坐标为