题目内容
一个直角三角形的一条直角边长为5,斜边长为13,则面积为
- A.30
- B.32.5
- C.60
- D.75
A
分析:先根据一个直角三角形的一条直角边长和斜边长,利用勾股定理计算出另一直角边长,然后即可求出此三角形面积.
解答:解;∵一个直角三角形的一条直角边长为5,斜边长为13,
∴由勾股定理得另一直角边长为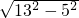 =12,
=12,
则S△= ×5×12=30.
×5×12=30.
故选A.
点评:此题主要考查学生对勾股定理和三角形面积的理解和掌握,解答此题的关键是先利用勾股定理计算出另一直角边长,然再求出此三角形面积.
分析:先根据一个直角三角形的一条直角边长和斜边长,利用勾股定理计算出另一直角边长,然后即可求出此三角形面积.
解答:解;∵一个直角三角形的一条直角边长为5,斜边长为13,
∴由勾股定理得另一直角边长为
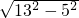 =12,
=12,则S△=
 ×5×12=30.
×5×12=30.故选A.
点评:此题主要考查学生对勾股定理和三角形面积的理解和掌握,解答此题的关键是先利用勾股定理计算出另一直角边长,然再求出此三角形面积.

练习册系列答案
相关题目
若一个直角三角形的一条直角边等于它的外接圆的半径,则该三角形的面积与其外接圆的面积的比为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|