题目内容
等腰△ABC中，AB=AC=5，BC=8，求底角∠B的四个三角函数值．分析：作AD⊥BC，交BC于点D，将△ABC分割成两个直角三角形，进而在Rt△ABD中，由勾股定理可得AD的值，根据三角函数的定义，可得底角∠B的四个三角函数值．
解答：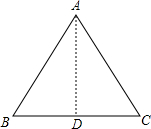
解：作AD⊥BC，交BC于点D，易得D为BC的中点，
在Rt△ABD中，有AB=5，BD=4；
由勾股定理可得：AD=3，
故cosB=
，sinB=
，tanB=
，cotB=
．
解：作AD⊥BC，交BC于点D，易得D为BC的中点，在Rt△ABD中，有AB=5，BD=4；
由勾股定理可得：AD=3，
故cosB=
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
| 4 |
| 4 |
| 3 |
点评：本题考查了解直角三角形的应用，要熟练掌握好边角之间的关系及三角函数的定义．
练习册系列答案
相关题目
24、等腰△ABC中，AB=AC，D为BC上的一动点，DE∥AC，DF∥AB，分别交AB于E，AC于F，则DE+DF是否随D点变化而变化？请说明理由．
如图，在等腰△ABC中，AB=AC，以AB为直径作⊙O交BC于D，交AC于E，过D点作DF⊥AC于F，有下列结论：
如图，在等腰△ABC中，AB=AC，∠A=50°，边AB的垂直平分线交边AC于点E，则∠EBC=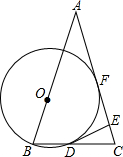
如图，在等腰△ABC中，AB=AC，O为AB上一点，以O为圆心，OB长为半径的圆交BC于D，DE⊥AC交AC于点E．