题目内容
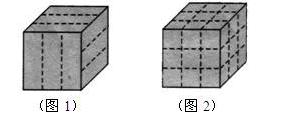
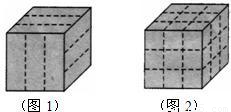
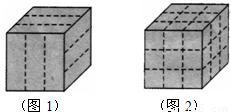
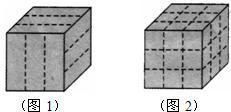
有一块表面是咖啡色、内部是白色、形状是正方体的烤面包.小明用刀在它的上表面、前面面和右侧表面沿虚线各切两刀(如图1),将它切成若干块小正方体形面包(如图2).
(1)小明从若干块小面包中任取一块,这块面包刚好只有两个面是咖啡色的概率是_________;
(2)小明和弟弟边吃边玩.游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,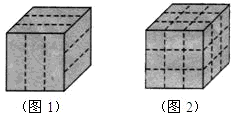 小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.
小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.
- A.
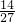 ,
, ,
,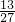
- B.
 ,
,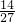 ,
,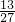
- C.
 ,
,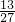 ,
,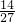
- D.
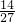 ,
,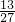 ,
,
B
分析:(1)根据将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,即可得出有两个面是咖啡色的概率;
(2)根据游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答: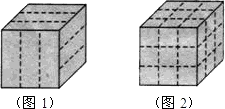 解:(1)按上述方法可将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,
解:(1)按上述方法可将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,
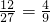 .
.
所以,所求概率是 .
.
(2)27块小面包中有8块是有且只有3个面是咖啡色,6块是有且只有1个面是咖啡色.
从中任取一块小面包,有且只有奇数个面为咖啡色的共有14块,剩余的面包块共有13块.
小明赢的概率是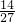 ,弟弟赢的概率是
,弟弟赢的概率是 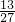 .
.
故选:B.
点评:此题考查的是游戏公平性的判断.判断游戏公平性就要计算每个人取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
分析:(1)根据将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,即可得出有两个面是咖啡色的概率;
(2)根据游戏是否公平,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
解答:
 解:(1)按上述方法可将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,
解:(1)按上述方法可将面包切成27块小面包,有且只有两个面是咖啡色的小面包有12块,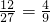 .
.所以,所求概率是
 .
.(2)27块小面包中有8块是有且只有3个面是咖啡色,6块是有且只有1个面是咖啡色.
从中任取一块小面包,有且只有奇数个面为咖啡色的共有14块,剩余的面包块共有13块.
小明赢的概率是
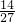 ,弟弟赢的概率是
,弟弟赢的概率是 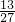 .
.故选:B.
点评:此题考查的是游戏公平性的判断.判断游戏公平性就要计算每个人取胜的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
有一块表面是咖啡色、内部是白色、形状是正方体的烤面包.小明用刀在它的上表面、前面面和右侧表面沿虚线各切两刀(如图1),将它切成若干块小正方体形面包(如图2).
(1)小明从若干块小面包中任取一块,这块面包刚好只有两个面是咖啡色的概率是_________;
(2)小明和弟弟边吃边玩.游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时, 小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.( )
小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.( )
(1)小明从若干块小面包中任取一块,这块面包刚好只有两个面是咖啡色的概率是_________;
(2)小明和弟弟边吃边玩.游戏规则是:从中任取一块小面包,若它有奇数个面为咖啡色时,
 小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.( )
小明赢;否则,弟弟赢.则小明和弟弟赢的概率各是________.( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 小明赢;否则,弟弟赢.你认为这样的游戏规则公平吗?为什么?如果不公平,请你修改游戏规则,使之公平.
小明赢;否则,弟弟赢.你认为这样的游戏规则公平吗?为什么?如果不公平,请你修改游戏规则,使之公平.