Question

如图，正方形ABCD的面积为l2，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，PD+PE的和最小，则这个最小值为_______．
 

Answer 1

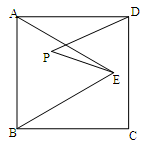
试题分析：先根据正方形ABCD的面积为12，△ABE是等边三角形求得BE=AB=，连接PB，则PD=PB，因此当P、B、E在一直线的时候，PD+PE的和最小，从而可以求得结果.
解：∵正方形ABCD的面积为12，△ABE是等边三角形，
∴BE=AB=
连接PB，则PD=PB，

那么PD+PE=PB+PE，
因此当P、B、E在一直线的时候，PD+PE的和最小，
也就是PD+PE=PB+PE=BE=AB=.
点评：此类问题是初中数学的重点，是中考中比较常见的知识点，一般难度不大，需熟练掌握.