题目内容
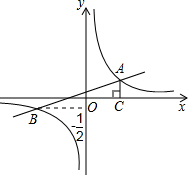
 如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
如图,已知在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数 (m≠0)的图象相交于A、B两点,且点B的纵坐标为
(m≠0)的图象相交于A、B两点,且点B的纵坐标为 ,过点A作AC⊥x轴于点C,AC=1,OC=2.
,过点A作AC⊥x轴于点C,AC=1,OC=2.求:(1)求反比例函数和一次函数的关系式;
(2)直接写出反比例函数值大于一次函数值时x的取值范围.
【答案】分析:(1)首先根据已知条件确定点A的坐标为,然后代入反比例函数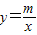 (m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;
(m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;
(2)根据(1)中的函数关系式结合图象即可写出反比例函数值大于一次函数值时x的取值范围.
解答:解:(1)∵AC=1,OC=2,且点A在第一象限
∴点A的坐标为(2,1)
∵点A在反比例函数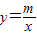 (m≠0)的图象上,∴m=2
(m≠0)的图象上,∴m=2
∴反比例函数关系式为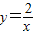
∵点B在反比例函数图象上,且点B的纵坐标为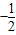
∴x=-4即点B的坐标为(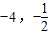 )
)
∵A、B两点均在直线y=kx+b上
∴ ,
,
∴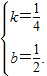 ,
,
∴一次函数的关系式是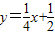 ;
;
(2)当反比例函数值大于一次函数值时,则x的取值范围是x<-4或0<x<2.
点评:本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.
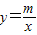 (m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;
(m≠0)确定m的值,接着求出点B的纵坐标,再利用待定系数法即可求出一次函数的关系式;(2)根据(1)中的函数关系式结合图象即可写出反比例函数值大于一次函数值时x的取值范围.
解答:解:(1)∵AC=1,OC=2,且点A在第一象限
∴点A的坐标为(2,1)
∵点A在反比例函数
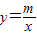 (m≠0)的图象上,∴m=2
(m≠0)的图象上,∴m=2∴反比例函数关系式为
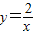
∵点B在反比例函数图象上,且点B的纵坐标为
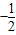
∴x=-4即点B的坐标为(
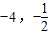 )
)∵A、B两点均在直线y=kx+b上
∴
 ,
,∴
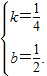 ,
,∴一次函数的关系式是
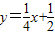 ;
;(2)当反比例函数值大于一次函数值时,则x的取值范围是x<-4或0<x<2.
点评:本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取0.

练习册系列答案
相关题目
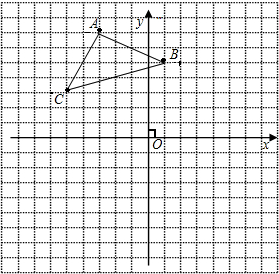 如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),
如图,已知在平面直角坐标系中,△ABC的顶点坐标为A(-3,7),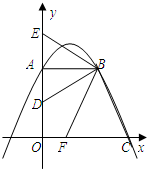 边分别交y轴的正半轴、x轴的正半轴于点E和F.
边分别交y轴的正半轴、x轴的正半轴于点E和F.
 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2= 如图,已知在平面直角坐标系中,△ABC的位置如图所示
如图,已知在平面直角坐标系中,△ABC的位置如图所示