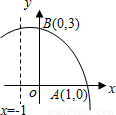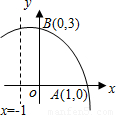题目内容
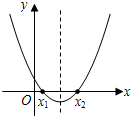 如图,函数y=x2-2x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-2时,函数值( )
如图,函数y=x2-2x+m(m为常数)的图象如图,如果x=a时,y<0;那么x=a-2时,函数值( )分析:把x=a代入函数y=x2-2x+m中求出函数a、a-2与0的关系,进而确定x=a-2时,函数y=x2-2x+m的值.
解答:解:x=a代入函数y=x2-2x+m中得:y=a2-2a+m=a(a-2)+m,
∵x=a时,y<0,
∴a(a-2)+m<0,
由图象可知:m>0,
∴a(a-2)<0,
又∵x=a时,y<0,
∴a>0则a-2<0,
由图象可知:x=0时,y=m,
又∵x<1时y随x的增大而减小,
∴x=a-2时,y>m.
故选:D.
∵x=a时,y<0,
∴a(a-2)+m<0,
由图象可知:m>0,
∴a(a-2)<0,
又∵x=a时,y<0,
∴a>0则a-2<0,
由图象可知:x=0时,y=m,
又∵x<1时y随x的增大而减小,
∴x=a-2时,y>m.
故选:D.
点评:此题主要考查了二次函数与不等式(组),利用数形结合法、假设法都是解决数学习题常用的方法,巧妙运用解题方法可以节省解题时间.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
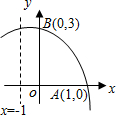 如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )
如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )| A、顶点坐标为(-1,4) | B、函数的解析式为y=-x2-2x+3 | C、当x<0时,y随x的增大而增大 | D、抛物线与x轴的另一个交点是(-3,0) |
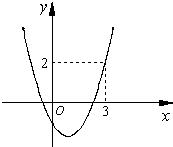 17、如图是函数y=x2+bx-1的图象,根据图象提供的信息,确定使-1≤y≤2的自变量x的取值范围是
17、如图是函数y=x2+bx-1的图象,根据图象提供的信息,确定使-1≤y≤2的自变量x的取值范围是