题目内容
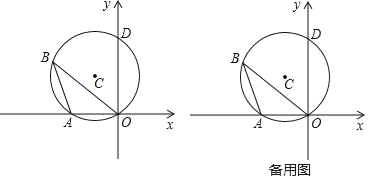
【题目】如图,已知点A,B分别是反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO=
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO=![]() ,则k的值为( )
,则k的值为( )
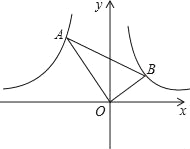
A. 2 B. ﹣2 C. 4 D. ﹣4
【答案】D
【解析】
首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A,B分别在反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,即可得S△OBD=
(x>0)的图象上,即可得S△OBD=![]() ,S△AOC=
,S△AOC=![]() |k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
|k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
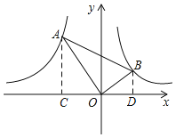
∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
又∵∠AOB=90°,tan∠BAO=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() ,
,
解得k=±4,
又∵k<0,
∴k=-4,
故选:D.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目