题目内容
阅读下面的文字,解答问题:
大家知道 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用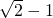 来表示
来表示 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为 的整数部分是1,将这个数减去其整数部分,所得的差就是小数部分.
的整数部分是1,将这个数减去其整数部分,所得的差就是小数部分.
又例如:因为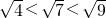 ,即
,即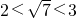 ,
,
所以 的整数部分为2,小数部分为
的整数部分为2,小数部分为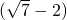 .
.
请解答:
(1) 如果 的整数部分为a,那么a=________.如果
的整数部分为a,那么a=________.如果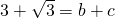 ,其中b是整数,且0<c<1,那么b=________,c=________.
,其中b是整数,且0<c<1,那么b=________,c=________.
(2) 将(1)中的a、b作为直角三角形的两条直角边,请你计算第三边的长度.
解:(1)∵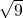 <
<
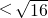 即3<
即3< <4,
<4,
所以 的整数部分为3,
的整数部分为3,
当3+ =b+c且b为整数,0<c<1,
=b+c且b为整数,0<c<1,
∴c= -1,b=4;
-1,b=4;
(2)a=3,b=4,
在直角三角形中,斜边的平方等于两直角边的平方和,
即斜边的长为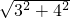 =5,
=5,
即第三边为5,
故答案为:(1)3,4, -1.(2)第三边的长为5.
-1.(2)第三边的长为5.
分析:(1)按照题干中给出的判定方法可以判定3< <4;
<4;
(2)在直角三角形中,已知两直角边的长度,根据勾股定理可以计算斜边的长度.
点评:本题考查了勾股定理在直角三角形中的运用,考查了无理数大小的估算,本题中正确的计算a、b的值是解题的关键.
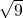 <
<
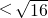 即3<
即3< <4,
<4,所以
 的整数部分为3,
的整数部分为3,当3+
 =b+c且b为整数,0<c<1,
=b+c且b为整数,0<c<1,∴c=
 -1,b=4;
-1,b=4;(2)a=3,b=4,
在直角三角形中,斜边的平方等于两直角边的平方和,
即斜边的长为
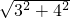 =5,
=5,即第三边为5,
故答案为:(1)3,4,
 -1.(2)第三边的长为5.
-1.(2)第三边的长为5.分析:(1)按照题干中给出的判定方法可以判定3<
 <4;
<4;(2)在直角三角形中,已知两直角边的长度,根据勾股定理可以计算斜边的长度.
点评:本题考查了勾股定理在直角三角形中的运用,考查了无理数大小的估算,本题中正确的计算a、b的值是解题的关键.

练习册系列答案
相关题目