题目内容
【题目】如图所示,△ABO中,A,B两点的坐标分别为(2,4),(7,2),C,G,F,E分别为过A,B两点所作的y轴、x轴的垂线与y轴、x轴的交点.求△AOB的面积.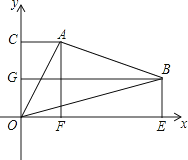
【答案】解:∵A(2,4),B(7,2),
∴AC=2、CO=4、OE=7、BE=2、AF=4、EF=OE﹣OF=7﹣2=5,
由图可知,S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE ,
=2×4+![]() (2+4)×5﹣
(2+4)×5﹣![]() ×2×4﹣
×2×4﹣![]() ×7×2,
×7×2,
=8+15﹣4﹣7,
=23﹣11,
=12.
【解析】根据点A、B的坐标求出AC、CO、OE、BE、AF、EF的长度,然后根据S△AOB=S矩形ACOF+S梯形AFEB﹣S△ACO﹣S△BOE列式计算即可得解.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目