题目内容
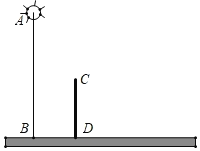
【题目】如图所示,灯在距地面6米的A处,与灯柱AB相距3米的地方有一长3米的木棒CD直立于地面.
(1)在图中画出木棒CD的影子,并求出它的长度;
(2)当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时,其影子的变化有什么规律?你能求出其影长的取值范围吗?
【答案】(1)作图见解析,影子DE的长度为3米;(2)当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时,其影子的变化规律为:先变长,后变短;当木棒CD与经过C'点的光线垂直时,影子DE'最长,3米≤影长≤5米.
【解析】
(1)根据中心投影即可在图中画出木棒CD的影子,根据三角形相似即可求出它的长度;
(2)当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时,其影子的变化先变长,后变短,根据相似三角形的性质即可求出其影长的取值范围.
如图,
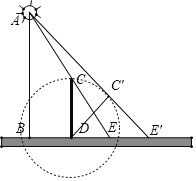
(1)DE即为木棒CD的影子,
根据题意,得
AB=6,CD=3,BD=3.
∵CD∥AB,∴![]()
即![]() ,
,
解得:DE=3.
所以影子DE的长度为3米;
(2)当木棒绕其与地面的固定端点D按顺时针方向旋转到地面时,
其影子的变化规律为:先变长,后变短;
当木棒CD与经过C'点的光线垂直时,影子DE'最长.
如图DC'⊥AE',∴∠E'C'D=∠ABE'=90°,
∠C'E'D=∠AE'B,∴△E'C'D∽△E'BA,
∴![]()
即BE'=2C'E'
设C'E'=x,则BE'=2x,
∴DE'=BE'﹣BD=2x﹣3,
在Rt△DE'C'中,根据勾股定理,得(2x﹣3)2=32+x2
解得:x=0或4,
∴DE'=5,
所以其影长的取值范围是:大于或等于3米,小于或等于5米.

练习册系列答案
相关题目